题目内容
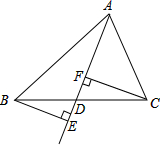 如图,在△ABC中,BE⊥AD于点E,CF⊥AD于点F,且BE=CF,那么BD与DC相等吗?你能说明理由吗?
如图,在△ABC中,BE⊥AD于点E,CF⊥AD于点F,且BE=CF,那么BD与DC相等吗?你能说明理由吗?解:BD=DC.
∵BE⊥AD于点E,CF⊥AD于点F,
∴∠
在

∴
∴BD=DC
考点:全等三角形的判定与性质
专题:推理填空题
分析:可以通过证明△BDE和△CDF全等来确定其为中线,即BD=CD.
解答:解:BD=CD,
理由如下:
∵BE⊥AD,CF⊥AD,
∴∠BED=∠CFD=90°,
在△BDE和△CDF中,
,
∴△BDE≌△CDF(AAS),
∴BD=CD(全等三角形的对应边相等)
理由如下:
∵BE⊥AD,CF⊥AD,
∴∠BED=∠CFD=90°,
在△BDE和△CDF中,
|
∴△BDE≌△CDF(AAS),
∴BD=CD(全等三角形的对应边相等)
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.做题时要根据实际情况灵活运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列说法不正确的是( )
| A、等腰梯形的对角线相等 |
| B、矩形的对角线互相垂直 |
| C、对角线互相垂直平分的四边形是菱形 |
| D、一组对边平行且相等的四边形是平行四边形 |
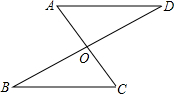 如图,已知AC与BD交于点O,AD∥BC,且AD=BC,求证:BO=DO.
如图,已知AC与BD交于点O,AD∥BC,且AD=BC,求证:BO=DO.
 如图,两块相同的直角三角板拼成一个图形.
如图,两块相同的直角三角板拼成一个图形. 如图,在△ABC中,AB=AC,D是△ABC外的一点,且BD=CD.求证:AD垂直平分BC.
如图,在△ABC中,AB=AC,D是△ABC外的一点,且BD=CD.求证:AD垂直平分BC. 已知圆上两点A,B(如图),用直尺和圆规求作以AB为一边的圆的内接等腰三角形,这样的三角形能作几个?
已知圆上两点A,B(如图),用直尺和圆规求作以AB为一边的圆的内接等腰三角形,这样的三角形能作几个?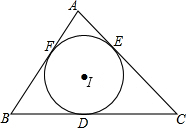 如图,设△ABC的边BC=a,CA=b,AB=c,s=
如图,设△ABC的边BC=a,CA=b,AB=c,s=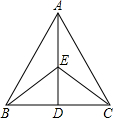 已知:如图,D是△ABC中BC边上一点,EB=EC,∠ABE=∠ACE,求证:AB=AC.
已知:如图,D是△ABC中BC边上一点,EB=EC,∠ABE=∠ACE,求证:AB=AC.