题目内容
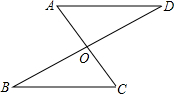 如图,已知AC与BD交于点O,AD∥BC,且AD=BC,求证:BO=DO.
如图,已知AC与BD交于点O,AD∥BC,且AD=BC,求证:BO=DO.证明:∵AD∥BC(已知),
∴∠A=
∠D=
在

∴
∴BO=DO
考点:全等三角形的判定与性质
专题:推理填空题
分析:根据两直线平行,内错角相等和全等三角形的判定与性质分别填空即可.
解答:证明:∵AD∥BC(已知),
∴∠A=∠C,( ),
∠D=∠B,(两直线平行,内错角相等).
在△ADO和△CBO中,
,
∴△ADO≌△CBO(ASA).
∴BO=DO(全等三角形对应边相等).
故答案为:∠C,(两直线平行,内错角相等),∠B,(两直线平行,内错角相等),△ADO和△CBO,△ADO,△CBO(ASA),(全等三角形对应边相等).
∴∠A=∠C,( ),
∠D=∠B,(两直线平行,内错角相等).
在△ADO和△CBO中,
|
∴△ADO≌△CBO(ASA).
∴BO=DO(全等三角形对应边相等).
故答案为:∠C,(两直线平行,内错角相等),∠B,(两直线平行,内错角相等),△ADO和△CBO,△ADO,△CBO(ASA),(全等三角形对应边相等).
点评:本题考查了全等三角形的判定与性质,平行线的性质,主要是对逻辑推理能力的训练,熟记全等三角形的判定方法是解题的关键.

练习册系列答案
相关题目
下列变形过程属于因式分解变形的个数是( )
①a2x+b2x=x(a2+b2);
②x2-1=(x+1)(x-1);
③(3x-1)(4x+3)=12x2+5x+3;
④a+1=a(1+
);
⑤4x2+16x-1=4x(x+4)+1;
⑥
ax+
bx=
x(a+b).
①a2x+b2x=x(a2+b2);
②x2-1=(x+1)(x-1);
③(3x-1)(4x+3)=12x2+5x+3;
④a+1=a(1+
| 1 |
| a |
⑤4x2+16x-1=4x(x+4)+1;
⑥
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| A、3个 | B、4个 | C、5个 | D、6个 |
半径为5的圆,其圆心在坐标原点,则下列各点中,在该圆上的是( )
| A、(3,3) |
| B、(3,4) |
| C、(4,4) |
| D、(4,5) |
在Rt△ABC中,∠ACB=90°,若sinB=
,则tanA=( )
| 5 |
| 13 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 已知△ABC,如图,画出中线AD和角平分线BE.
已知△ABC,如图,画出中线AD和角平分线BE.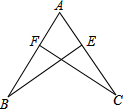 如图,在△ABE和△ACF中,AB=AC,BF=CE.求证:
如图,在△ABE和△ACF中,AB=AC,BF=CE.求证: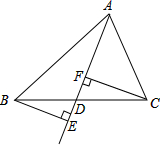 如图,在△ABC中,BE⊥AD于点E,CF⊥AD于点F,且BE=CF,那么BD与DC相等吗?你能说明理由吗?
如图,在△ABC中,BE⊥AD于点E,CF⊥AD于点F,且BE=CF,那么BD与DC相等吗?你能说明理由吗?