题目内容
 如图,AB=CD,AE=DF,CE=BF,判断EC和BF的位置关系,并说明理由.
如图,AB=CD,AE=DF,CE=BF,判断EC和BF的位置关系,并说明理由.考点:全等三角形的判定与性质
专题:计算题
分析:EC与BF平行,理由为:由AB=DC,利用等式的性质得到AC=BD,利用SSS得到三角形AEC与三角形DFB全等,利用全等三角形对应角相等得到内错角相等,利用内错角相等两直线平行即可得证.
解答:答:EC∥BF,理由为:
证明:∵AB=DC,
∴AB+BC=DC+BC,即AC=DB,
在△AEC和△FDB中,
,
∴△AEC≌△FDB(SSS),
∴∠ACE=∠DBF,
∴EC∥BF.
证明:∵AB=DC,
∴AB+BC=DC+BC,即AC=DB,
在△AEC和△FDB中,
|
∴△AEC≌△FDB(SSS),
∴∠ACE=∠DBF,
∴EC∥BF.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
弦心距为4,弦长为8的弦所对的劣弧长是( )
| A、8π | ||
| B、4π | ||
C、
| ||
D、2
|
某抗震蓬的顶部是圆锥形,这个圆锥的底面直径为10米,母线长为6米,为了防雨,需要在它的顶部铺上油毡,所需油毡的面积至少是( )
| A、30л米2 |
| B、55л米2 |
| C、30米2 |
| D、60л米2 |
 如图所示,已知AD=AE,BD=CE,试探究AB与AC的大小关系,并说明理由.
如图所示,已知AD=AE,BD=CE,试探究AB与AC的大小关系,并说明理由.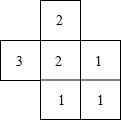 (1)一个由相同小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上小立方块的个数,画出该几何体的主视图和左视图
(1)一个由相同小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上小立方块的个数,画出该几何体的主视图和左视图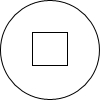 一个零件的主视图如图,其中圆的直径为300mm,正方形中孔的中心位于圆的圆心,正方形的边长为120mm.
一个零件的主视图如图,其中圆的直径为300mm,正方形中孔的中心位于圆的圆心,正方形的边长为120mm.