题目内容
弦心距为4,弦长为8的弦所对的劣弧长是( )
| A、8π | ||
| B、4π | ||
C、
| ||
D、2
|
考点:弧长的计算
专题:
分析:连接OA、OB,根据垂径定理求出AC=BC=4,推出∠AOB=90°,在Rt△ACO中,由勾股定理求出OA,根据弧长公式求出即可.
解答:解:
如图,连接OA、OB,
∵OC⊥AB,OC过O,AB=8,
∴AC=BC=4,
∵OC=4,
∴AC=BC=OD,
∴∠AOB=90°,
在Rt△ACO中,由勾股定理得:OA=
=4
,
劣弧AB的长是
=2
π,
故选D.

如图,连接OA、OB,
∵OC⊥AB,OC过O,AB=8,
∴AC=BC=4,
∵OC=4,
∴AC=BC=OD,
∴∠AOB=90°,
在Rt△ACO中,由勾股定理得:OA=
| 42+42 |
| 2 |
劣弧AB的长是
90π×4
| ||
| 180 |
| 2 |
故选D.
点评:本题考查了弧长公式垂径定理,勾股定理的应用,主要考查学生的理解能力和计算能力,注意:半径为R,圆心角为n°所对的弧的长度是
.
| nπR |
| 180 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知⊙O的直径为10,OP=6,则点P与⊙O的位置关系是( )
| A、点P在⊙O内 |
| B、点P在⊙O上 |
| C、点P在⊙O外 |
| D、不能确定 |
 如图,在边长为1的正方形组成的网格中,△ABC的顶点都在格点上,将△ABC绕点C顺时针旋转60°,则顶点A所经过的路径长为
如图,在边长为1的正方形组成的网格中,△ABC的顶点都在格点上,将△ABC绕点C顺时针旋转60°,则顶点A所经过的路径长为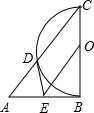 如图,以Rt△ABC的直角边BC为直径作半圆O交斜边于D,OE∥AC,交AB于E,连接DE.
如图,以Rt△ABC的直角边BC为直径作半圆O交斜边于D,OE∥AC,交AB于E,连接DE. 如图,AB=CD,AE=DF,CE=BF,判断EC和BF的位置关系,并说明理由.
如图,AB=CD,AE=DF,CE=BF,判断EC和BF的位置关系,并说明理由.