题目内容
4.解方程组$\left\{\begin{array}{l}{ax+by=2}\\{cx-7y=8}\end{array}\right.$时,应该正确地解得$\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$,小明由于看错了系数c,得到的解为$\left\{\begin{array}{l}{x=-2}\\{y=2}\end{array}\right.$则a-b-c=1.分析 把正确和错误结果代入方程组第一个方程求出a与b的值,将正确结果代入第二个方程求出c的值,即可求出所求.
解答 解:把$\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$与$\left\{\begin{array}{l}{x=-2}\\{y=2}\end{array}\right.$代入得:$\left\{\begin{array}{l}{3a-2b=2}\\{-a+b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=4}\\{b=5}\end{array}\right.$,
把$\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$代入得:3c+14=8,
解得:c=-2,
则a-b-c=4-5+2=1.
故答案为:1
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.

练习册系列答案
相关题目
15. 为了解2017年北海市九年级学生学业考试体育成绩,现随机抽取部分学生的体育成绩(A:60分;B:59-54分;C:53-48分;D:47-36分;E:35-0分)进行分段统计如下:
为了解2017年北海市九年级学生学业考试体育成绩,现随机抽取部分学生的体育成绩(A:60分;B:59-54分;C:53-48分;D:47-36分;E:35-0分)进行分段统计如下:
学业考试体育成绩(分数段)统计表/图
根据上面提供的信息,回答下列问题:
(1)在统计表中,a的值为60,b的值为0.15;
(2)将统计图补充完整;
(3)如果把成绩在48分以上(含48分)定为优秀,那么北海市在2017年8580名九年级学生中体育成绩为优秀的学生人数约有多少名?
 为了解2017年北海市九年级学生学业考试体育成绩,现随机抽取部分学生的体育成绩(A:60分;B:59-54分;C:53-48分;D:47-36分;E:35-0分)进行分段统计如下:
为了解2017年北海市九年级学生学业考试体育成绩,现随机抽取部分学生的体育成绩(A:60分;B:59-54分;C:53-48分;D:47-36分;E:35-0分)进行分段统计如下:学业考试体育成绩(分数段)统计表/图
| 分数段 | 人数(人) | 频率 |
| A | 48 | 0.2 |
| B | a | 0.25 |
| C | 84 | 0.35 |
| D | 36 | b |
| E | 12 | 0.05 |
(1)在统计表中,a的值为60,b的值为0.15;
(2)将统计图补充完整;
(3)如果把成绩在48分以上(含48分)定为优秀,那么北海市在2017年8580名九年级学生中体育成绩为优秀的学生人数约有多少名?
19. 如图,AB∥CD∥EF,则下列各式中正确的是( )
如图,AB∥CD∥EF,则下列各式中正确的是( )
 如图,AB∥CD∥EF,则下列各式中正确的是( )
如图,AB∥CD∥EF,则下列各式中正确的是( )| A. | ∠1=180°-∠3 | B. | ∠1=∠3-∠2 | C. | ∠2+∠3=180°-∠1 | D. | ∠2+∠3=180°+∠1 |
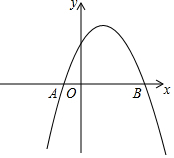 如图,已知抛物线y=-x2+bx+c经过A(-1,0),B(3,0)两点.
如图,已知抛物线y=-x2+bx+c经过A(-1,0),B(3,0)两点. 如图,直线y=kx+b(k≠0)与x轴交于点(-4,0),则关于x的不等式kx+b>0的解集是x>-4.
如图,直线y=kx+b(k≠0)与x轴交于点(-4,0),则关于x的不等式kx+b>0的解集是x>-4.