题目内容
如图,已知正比例函数y=
x与反比例函数y=
(k>0)的图象交于A、B两点,且点A的横坐标为4.
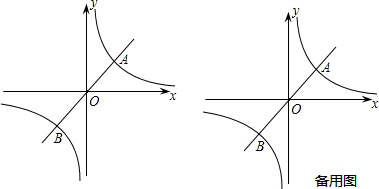
(1)求k的值;
(2)根据图象直接写出正比例函数值小于反比例函数值时x的取值范围;
(3)过原点O的另一条直线l交双曲线y=
(k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为24,求点P的坐标.
| 1 |
| 2 |
| k |
| x |

(1)求k的值;
(2)根据图象直接写出正比例函数值小于反比例函数值时x的取值范围;
(3)过原点O的另一条直线l交双曲线y=
| k |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)先将x=4代入正比例函数y=
x,可得出y=2,求得点A(4,2),再根据点A与B关于原点对称,得出B点坐标,即可得出k的值;
(2)正比例函数的值小于反比例函数的值即正比例函数的图象在反比例函数的图象下方,根据图形可知在交点的右边正比例函数的值小于反比例函数的值.
(3)由于双曲线是关于原点的中心对称图形,因此以A、B、P、Q为顶点的四边形应该是平行四边形,那么△POA的面积就应该是四边形面积的四分之一即6.可根据双曲线的解析式设出P点的坐标,然后表示出△POA的面积,由于△POA的面积为6,由此可得出关于P点横坐标的方程,即可求出P点的坐标.
| 1 |
| 2 |
(2)正比例函数的值小于反比例函数的值即正比例函数的图象在反比例函数的图象下方,根据图形可知在交点的右边正比例函数的值小于反比例函数的值.
(3)由于双曲线是关于原点的中心对称图形,因此以A、B、P、Q为顶点的四边形应该是平行四边形,那么△POA的面积就应该是四边形面积的四分之一即6.可根据双曲线的解析式设出P点的坐标,然后表示出△POA的面积,由于△POA的面积为6,由此可得出关于P点横坐标的方程,即可求出P点的坐标.
解答: (1)∵点A在正比例函数y=
(1)∵点A在正比例函数y=
x上,
∴把x=4代入正比例函数y=
x,
解得y=2,∴点A(4,2),
∵点A与B关于原点对称,
∴B点坐标为(-4,-2),
把点A(4,2)代入反比例函数y=
,得k=8,
(2)由交点坐标,根据图象直接写出正比例函数值小于反比例函数值时x的取值范围,-4<x<0或x>2;
(3)∵反比例函数图象是关于原点O的中心对称图形,
∴OP=OQ,OA=OB,
∴四边形APBQ是平行四边形,
∴S△POA=S平行四边形APBQ×
=
×24=6,
设点P的横坐标为m(m>0且m≠4),
得P(m,
),
过点P、A分别做x轴的垂线,垂足为E、F,
∵点P、A在双曲线上,
∴S△POE=S△AOF=4,
若0<m<4,如图,
∵S△POE+S梯形PEFA=S△POA+S△AOF,
∴S梯形PEFA=S△POA=6.
∴
(2+
)•(4-m)=6.
∴m1=2,m2=-8(舍去),
∴P(2,4);
 若m>4,如图,
若m>4,如图,
∵S△AOF+S梯形AFEP=S△AOP+S△POE,
∴S梯形PEFA=S△POA=6.
∴
(2+
)•(m-4)=6,
解得m1=8,m2=-2(舍去),
∴P(8,1).
∴点P的坐标是P(2,4)或P(8,1).
 (1)∵点A在正比例函数y=
(1)∵点A在正比例函数y=| 1 |
| 2 |
∴把x=4代入正比例函数y=
| 1 |
| 2 |
解得y=2,∴点A(4,2),
∵点A与B关于原点对称,
∴B点坐标为(-4,-2),
把点A(4,2)代入反比例函数y=
| k |
| x |
(2)由交点坐标,根据图象直接写出正比例函数值小于反比例函数值时x的取值范围,-4<x<0或x>2;
(3)∵反比例函数图象是关于原点O的中心对称图形,
∴OP=OQ,OA=OB,
∴四边形APBQ是平行四边形,
∴S△POA=S平行四边形APBQ×
| 1 |
| 4 |
| 1 |
| 4 |

设点P的横坐标为m(m>0且m≠4),
得P(m,
| 8 |
| m |
过点P、A分别做x轴的垂线,垂足为E、F,
∵点P、A在双曲线上,
∴S△POE=S△AOF=4,
若0<m<4,如图,
∵S△POE+S梯形PEFA=S△POA+S△AOF,
∴S梯形PEFA=S△POA=6.
∴
| 1 |
| 2 |
| 8 |
| m |
∴m1=2,m2=-8(舍去),
∴P(2,4);
 若m>4,如图,
若m>4,如图,∵S△AOF+S梯形AFEP=S△AOP+S△POE,
∴S梯形PEFA=S△POA=6.
∴
| 1 |
| 2 |
| 8 |
| m |
解得m1=8,m2=-2(舍去),
∴P(8,1).
∴点P的坐标是P(2,4)或P(8,1).
点评:本题考查了待定系数法求反比例函数与一次函数的解析式和反比例函数y=
中k的几何意义.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.利用数形结合的思想,求得三角形的面积.
| k |
| x |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 如图,已知AB∥CD,∠A=100°,CB平分∠ACD,求∠ACD、∠ABC的度数.
如图,已知AB∥CD,∠A=100°,CB平分∠ACD,求∠ACD、∠ABC的度数. 如图,在半径为
如图,在半径为