题目内容
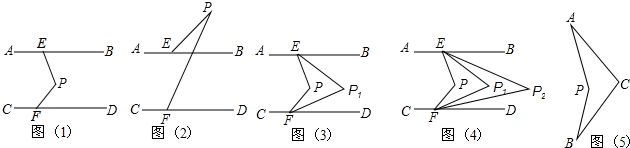
如图(1),直线AB∥CD,点P在两平行线之间,点E在AB上,点F在CD上,连结PE,PF.
(1)∠PEB,∠PFD,∠EPF满足的数量关系是 ,并说明理由.
(2)如图(2),若点P在直线AB上时,∠PEB,∠PFD,∠EPF满足的数量关系是 (不需说明理由)
(3)如图(3),在图(1)基础上,P1E平分∠PEB,P1F平分∠PFD,若设∠PEB=x°,∠PFD=y°.则∠P1= (用x,y的代数式表示),若P2E平分∠P1EB,P2F平分∠P1FD,可得∠P2,P3E平分∠P2EB,P3F平分∠P2FD,可得∠P3…,依次平分下去,则∠Pn= .
(4)科技活动课上,雨轩同学制作了一个图(5)的“飞旋镖”,经测量发现∠PAC=28°,∠PBC=30°,他很想知道∠APB与∠ACB的数量关系,你能告诉他吗?说明理由.
(1)∠PEB,∠PFD,∠EPF满足的数量关系是
(2)如图(2),若点P在直线AB上时,∠PEB,∠PFD,∠EPF满足的数量关系是
(3)如图(3),在图(1)基础上,P1E平分∠PEB,P1F平分∠PFD,若设∠PEB=x°,∠PFD=y°.则∠P1=
(4)科技活动课上,雨轩同学制作了一个图(5)的“飞旋镖”,经测量发现∠PAC=28°,∠PBC=30°,他很想知道∠APB与∠ACB的数量关系,你能告诉他吗?说明理由.

考点:平行线的性质
专题:规律型,探究型
分析:(1)过点P作PH∥AB∥CD,根据平行线的性质:两直线平行,内错角相等即可证得;
(2)若点P在直线AB上时,过P作AB的平行线,同理依据两直线平行,内错角相等即可证得;
(3)利用(1)的结论和角平分线的性质即可写出结论;
(4)过A、B分别作直线AE、BF,使AE∥BF,利用(1)的结论即可求解.
(2)若点P在直线AB上时,过P作AB的平行线,同理依据两直线平行,内错角相等即可证得;
(3)利用(1)的结论和角平分线的性质即可写出结论;
(4)过A、B分别作直线AE、BF,使AE∥BF,利用(1)的结论即可求解.
解答:解:(1)∠PEB,∠PFD,∠P满足的数量关系是∠P=∠PEB+∠PFD
理由如下:过点P作PH∥AB∥CD
∴∠PEB=∠EPH,∠PFD=∠FPH
而∠EPF=∠EPH+∠FPH
∴∠EPF=∠PEB+∠PFD
(2)如图(2),若点P在直线AB上时,
∠PEB,∠PFD,∠P满足的数量关系是∠PFD=∠PEB+∠P
(不需说明理由)
(3)∠P1=
(x+y)°(用x,y的代数式表示)
∠Pn=(
)n(x+y)°.
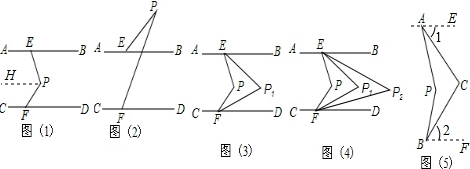
(4)解:∠APB=∠C+58°.理由如下:
过A、B分别作直线AE、BF,使AE∥BF.
如图,由(1)规律可知∠C=∠1+∠2.
∠APB=∠PAE+∠PBF
=(∠PAC+∠1)+(∠PBC+∠2)
=∠PAC+∠PBC+(∠1+∠2)
=∠C+58°
理由如下:过点P作PH∥AB∥CD
∴∠PEB=∠EPH,∠PFD=∠FPH
而∠EPF=∠EPH+∠FPH
∴∠EPF=∠PEB+∠PFD
(2)如图(2),若点P在直线AB上时,
∠PEB,∠PFD,∠P满足的数量关系是∠PFD=∠PEB+∠P
(不需说明理由)
(3)∠P1=
| 1 |
| 2 |
∠Pn=(
| 1 |
| 2 |
(4)解:∠APB=∠C+58°.理由如下:
过A、B分别作直线AE、BF,使AE∥BF.
如图,由(1)规律可知∠C=∠1+∠2.
∠APB=∠PAE+∠PBF
=(∠PAC+∠1)+(∠PBC+∠2)
=∠PAC+∠PBC+(∠1+∠2)
=∠C+58°

点评:本题考查了平行线的性质,正确理解题目之间的联系是关键.

练习册系列答案
相关题目
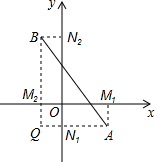 阅读材料:在平面直角坐标系中,已知x轴上两点A(x1,0),B(x2,0)的距离记作AB=|x1-x2|,如果A(x1,y1),B(x2,y2)是平面上任意两点,我们可以通过构造直角三角形来求AB间的距离.如图,过A,B分别向x轴、y轴作垂线AM1、AN1和BM2、BN2,垂足分别是M1、N1、M2、N2,直线AN1交BM2于点Q,在Rt△ABQ中,AQ=|x1-x2|,BQ=|y1-y2|,
阅读材料:在平面直角坐标系中,已知x轴上两点A(x1,0),B(x2,0)的距离记作AB=|x1-x2|,如果A(x1,y1),B(x2,y2)是平面上任意两点,我们可以通过构造直角三角形来求AB间的距离.如图,过A,B分别向x轴、y轴作垂线AM1、AN1和BM2、BN2,垂足分别是M1、N1、M2、N2,直线AN1交BM2于点Q,在Rt△ABQ中,AQ=|x1-x2|,BQ=|y1-y2|,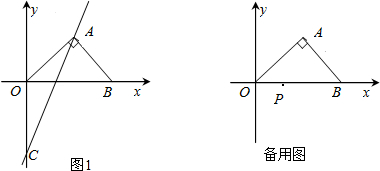
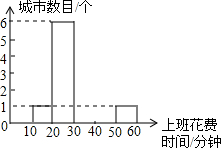 随着我国汽车产业的发展,城市道路拥堵问题日益严峻,某部门对15个城市的交通状况进行了调查,得到的数据如下表所示:
随着我国汽车产业的发展,城市道路拥堵问题日益严峻,某部门对15个城市的交通状况进行了调查,得到的数据如下表所示: 如图,平行四边形ABCD的顶点O,A,C的坐标分别是(0,0),(a,0),
如图,平行四边形ABCD的顶点O,A,C的坐标分别是(0,0),(a,0),