题目内容
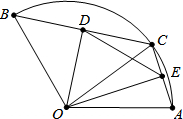 如图,在半径为2
如图,在半径为2| 3 |
(1)当BC=4时,求线段OD的长;
(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度;如果不存在,请说明理由.
考点:垂径定理,勾股定理,三角形中位线定理
专题:
分析:(1)求出BD,根据勾股定理求出OD即可;
(2)过点O作AB的垂直平分线,与AB交于点F,与弧AB交于点M,求出AF,得出AB长度,根据垂径定理得出D、E分别是BC、AC中点,根据三角形中位线求出即可.
(2)过点O作AB的垂直平分线,与AB交于点F,与弧AB交于点M,求出AF,得出AB长度,根据垂径定理得出D、E分别是BC、AC中点,根据三角形中位线求出即可.
解答:解:(1)∵OD⊥BC,
∴BD=
BC=2,
∴OD=
=
=2
.
(2)存在,DE是不变的,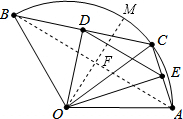
理由是:如图,连接AB,
过点O作AB的垂直平分线,与AB交于点F,与弧AB交于点M,
则OM平分∠AOB与弧AB,
∴∠AOF=60°,
在Rt△AOF中,∵∠AOF=60°,OA=2
,
∴AF=
OA=3,
∴AB=2AF=6,
由垂径定理可知,点D、E分别是BC和CA的中点,
∴DE是△ABC的中位线,
∴DE=
AB=3.
∴BD=
| 1 |
| 2 |
∴OD=
| BO2-BD2 |
(2
|
| 2 |
(2)存在,DE是不变的,

理由是:如图,连接AB,
过点O作AB的垂直平分线,与AB交于点F,与弧AB交于点M,
则OM平分∠AOB与弧AB,
∴∠AOF=60°,
在Rt△AOF中,∵∠AOF=60°,OA=2
| 3 |
∴AF=
| ||
| 2 |
∴AB=2AF=6,
由垂径定理可知,点D、E分别是BC和CA的中点,
∴DE是△ABC的中位线,
∴DE=
| 1 |
| 2 |
点评:本题考查了三角形中位线,垂径定理,勾股定理的应用,题目是一道比较典型的题目,难度适中.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
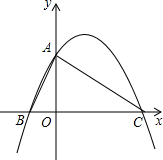 如图,二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点A(0,4),与x轴负半轴交于B,与正半轴交于点C(8,0),且∠BAC=90°.
如图,二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点A(0,4),与x轴负半轴交于B,与正半轴交于点C(8,0),且∠BAC=90°.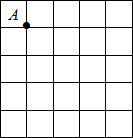 如图的正方形网格中,每个小正方形边长均为1,点A固定在格点(即小正方形的顶点)上,请按步骤要求作图并解答:
如图的正方形网格中,每个小正方形边长均为1,点A固定在格点(即小正方形的顶点)上,请按步骤要求作图并解答: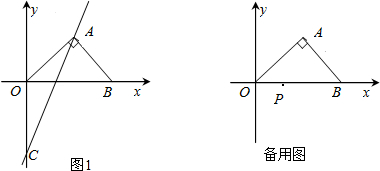
 如图,O为直线AB上一点,OC平分∠BOD,OE⊥OC,请说明下面两中结论的理由:
如图,O为直线AB上一点,OC平分∠BOD,OE⊥OC,请说明下面两中结论的理由: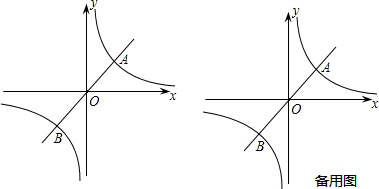
 如图,EG、AF、CB三条直线两两相交,AB、DE分别是∠GAD、∠FDC的角平分线,若AB=AD=DE,则∠DAC=
如图,EG、AF、CB三条直线两两相交,AB、DE分别是∠GAD、∠FDC的角平分线,若AB=AD=DE,则∠DAC=