题目内容
如图(1),在Rt△ABC,∠ACB=90°,分别以AB、BC为一边向外作正方形ABFG、BCED,连结AD、CF,AD与CF交于点M.
(1)△ABD是由△FBC绕点B按顺时针方向旋转 度而得到.
(2)如图2,已知AD=6,求四边形AFDC的面积.

(1)△ABD是由△FBC绕点B按顺时针方向旋转
(2)如图2,已知AD=6,求四边形AFDC的面积.

考点:旋转的性质,正方形的性质
专题:
分析:(1)根据旋转的性质∠ABF即为旋转角,所以旋转了90°.
(2)连接FD,由(1)的三角形全等,得到AD=FC,∠BAD=∠BFC,利用等式的性质及垂直定义得到AD与CF垂直,四边形AFDC面积=三角形ACD面积+三角形ACF面积+三角形DMF面积-三角形ACM面积,求出即可;
(2)连接FD,由(1)的三角形全等,得到AD=FC,∠BAD=∠BFC,利用等式的性质及垂直定义得到AD与CF垂直,四边形AFDC面积=三角形ACD面积+三角形ACF面积+三角形DMF面积-三角形ACM面积,求出即可;
解答:解:(1)∵四边形ABFG、BCED是正方形,
∴AB=FB,CB=DB,∠ABF=∠CBD=90°,
根据旋转的性质,
∴旋转角=90°.
(2)连接FD,设CF与AB交于点N,
∵△ABD≌△FBC,
∴AD=FC,∠BAD=∠BFC,
∴∠AMF=180°-∠BAD-∠CNA=180°-(∠BFC+∠BNF)=180°-90°=90°,
∴AD⊥CF,
∵AD=6,
∴FC=AD=6,
∴S四边形AFDC=S△ACD+S△ACF+S△DMF-S△ACM,
=
AD•CM+
CF•AM+
DM•FM-
AM•CM,
=3CM+3AM+
(6-AM)(6-CM)-
AM•CM,
=18;

故答案为:90°,18.
∴AB=FB,CB=DB,∠ABF=∠CBD=90°,
根据旋转的性质,
∴旋转角=90°.
(2)连接FD,设CF与AB交于点N,
∵△ABD≌△FBC,
∴AD=FC,∠BAD=∠BFC,
∴∠AMF=180°-∠BAD-∠CNA=180°-(∠BFC+∠BNF)=180°-90°=90°,
∴AD⊥CF,
∵AD=6,
∴FC=AD=6,
∴S四边形AFDC=S△ACD+S△ACF+S△DMF-S△ACM,
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=3CM+3AM+
| 1 |
| 2 |
| 1 |
| 2 |
=18;

故答案为:90°,18.
点评:此题考查了全等三角形的判定与性质,三角形、四边形的面积,以及三角形的三边关系,属于多知识点的四边形综合题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
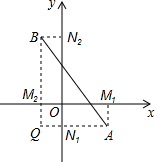 阅读材料:在平面直角坐标系中,已知x轴上两点A(x1,0),B(x2,0)的距离记作AB=|x1-x2|,如果A(x1,y1),B(x2,y2)是平面上任意两点,我们可以通过构造直角三角形来求AB间的距离.如图,过A,B分别向x轴、y轴作垂线AM1、AN1和BM2、BN2,垂足分别是M1、N1、M2、N2,直线AN1交BM2于点Q,在Rt△ABQ中,AQ=|x1-x2|,BQ=|y1-y2|,
阅读材料:在平面直角坐标系中,已知x轴上两点A(x1,0),B(x2,0)的距离记作AB=|x1-x2|,如果A(x1,y1),B(x2,y2)是平面上任意两点,我们可以通过构造直角三角形来求AB间的距离.如图,过A,B分别向x轴、y轴作垂线AM1、AN1和BM2、BN2,垂足分别是M1、N1、M2、N2,直线AN1交BM2于点Q,在Rt△ABQ中,AQ=|x1-x2|,BQ=|y1-y2|,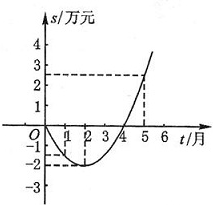 下面的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s和t之间的关系).根据图象提供的信息,解答下列问题:
下面的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s和t之间的关系).根据图象提供的信息,解答下列问题: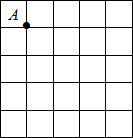 如图的正方形网格中,每个小正方形边长均为1,点A固定在格点(即小正方形的顶点)上,请按步骤要求作图并解答:
如图的正方形网格中,每个小正方形边长均为1,点A固定在格点(即小正方形的顶点)上,请按步骤要求作图并解答: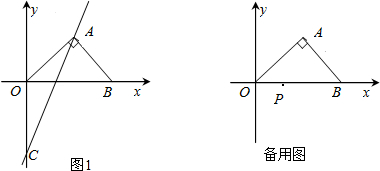
 如图,平行四边形ABCD的顶点O,A,C的坐标分别是(0,0),(a,0),
如图,平行四边形ABCD的顶点O,A,C的坐标分别是(0,0),(a,0),