题目内容
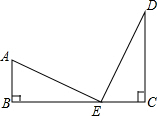 如图,Rt△ABE≌Rt△ECD,点B、E、C在同一直线上,则结论:
如图,Rt△ABE≌Rt△ECD,点B、E、C在同一直线上,则结论:①AE=ED;②AE⊥DE;③BC=AB+CD;④AB∥DC.
其中成立的是
考点:全等三角形的性质
专题:
分析:根据全等三角形的性质得出AE=DE,∠A=∠DEC,AB=CE,BE=CD,求出∠AEB+∠DEC=90°,求出∠AED=90°,即可判断①②③,根据平行线的判定即可判断④.
解答:解:∵Rt△ABE≌Rt△ECD,
∴AE=DE,∠A=∠DEC,∴①正确;
∵∠B=90°,
∴∠A+∠AEB=90°,
∴∠AEB+∠DEC=90°,
∴∠AED=90°,
∴AE⊥DE,∴②正确;
∵Rt△ABE≌Rt△ECD,
∴AB=CE,DC=BE,
∴BC=BE+CE=AB+DC,∴③正确;
∵∠B=∠C=90°,
∴∠B+∠C=180°,
∴AB∥CD,∴④正确;
故答案为:①②③④.
∴AE=DE,∠A=∠DEC,∴①正确;
∵∠B=90°,
∴∠A+∠AEB=90°,
∴∠AEB+∠DEC=90°,
∴∠AED=90°,
∴AE⊥DE,∴②正确;
∵Rt△ABE≌Rt△ECD,
∴AB=CE,DC=BE,
∴BC=BE+CE=AB+DC,∴③正确;
∵∠B=∠C=90°,
∴∠B+∠C=180°,
∴AB∥CD,∴④正确;
故答案为:①②③④.
点评:本题考查了全等三角形的性质和平行线的判定的应用,注意:全等三角形的对应边相等,对应角相等.

练习册系列答案
相关题目
下列是计算正确的是( )
| A、-8-3=-5 |
| B、-(-2)2=4 |
| C、-(x-y)=x+y |
| D、ab+2ba=3ab |
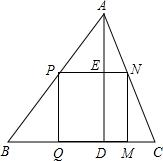 如图,△ABC是一块锐角三角形余料,其中BC=15cm,高AD=10cm,现在要把它裁剪成一个矩形材料备用,使矩形的一边在BC上,其余两个顶点分别在AB、AC上,若矩形的一边PN=9,求矩形另一边PQ的长.
如图,△ABC是一块锐角三角形余料,其中BC=15cm,高AD=10cm,现在要把它裁剪成一个矩形材料备用,使矩形的一边在BC上,其余两个顶点分别在AB、AC上,若矩形的一边PN=9,求矩形另一边PQ的长.