Question

20．如图，边长为3的正△ABC内接于⊙O，点P是$\widehat{AB}$上的动点，则PA+PB的最大值是（　　）

• A． 3$\sqrt{3}$
• B． 2$\sqrt{3}$
• C． $\sqrt{3}$
• D． $\frac{3}{2}$$\sqrt{3}$

Answer 1

分析 根据题意结合全等三角形的判定与性质得出当PC是⊙O的直径，此时PA+PB最大，进而结合等边三角形的性质得出PA+PB的最大值．

解答 解：如图所示：连接PC，BO，截取PE=AP，过点A作AF⊥BC于点F，
∵∠APC=60°，
∴△PEA为等边三角形，
∴AE=AP，∠PAE=60°，
而∠CAB=60°，
∴∠CAE=∠BAP，
在△CAE和△BAP
$\left\{\begin{array}{l}{AC=AB}\\{∠CAE=∠BAP}\\{AE=AP}\end{array}\right.$
∴△CAE≌△BAP（SAS），
∴PB=EC，
∴PB+PA=PC，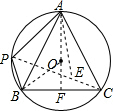
当PC是⊙O的直径，此时PA+PB最大，
即点P是弧BA的中点，
∵△ABC是⊙O的内接正三角形，
∴BF=FC=$\frac{3}{2}$，AC=3，
∴AF=$\frac{3\sqrt{3}}{2}$，
∴设F0=x，则AO=2x，则3x=$\frac{3\sqrt{3}}{2}$，
故AO=$\sqrt{3}$，
则PC=2$\sqrt{3}$，即PA+PB的最大值是2$\sqrt{3}$．
故选：B．

点评 此题主要考查了全等三角形的判定与性质以及等边三角形的性质等知识，正确得出点P是弧BA的中点，PA+PB最大是解题关键．