题目内容
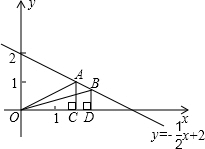 一次函数y=-
一次函数y=-| 1 |
| 2 |
考点:一次函数图象上点的坐标特征
专题:
分析:△AOC的面积S1已知,△BOD的面积S2可由关于a的函数表示,求出S2的取值范围,跟S1比较即可.
解答:解:把x=2代入y=-
x+2,
得y=-
×2+2=1,
即A(2,1),
则S1=
×2×1=1,
S2=
a×(-
a+2)=-
(a-2)2+1,
又0<a<4且a≠2,
所以S2<1=S1,即S1>S2,
故答案为S1>S2.
| 1 |
| 2 |
得y=-
| 1 |
| 2 |
即A(2,1),
则S1=
| 1 |
| 2 |
S2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
又0<a<4且a≠2,
所以S2<1=S1,即S1>S2,
故答案为S1>S2.
点评:本题考查的是一次函数图象上点的坐标特征,由一次函数确定坐标,根据坐标表示出面积并比较大小,另外还考查了二次函数的性质.

练习册系列答案
相关题目
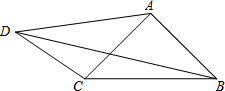 如图,在四边形ABCD中,AD=5,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD的长为( )
如图,在四边形ABCD中,AD=5,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
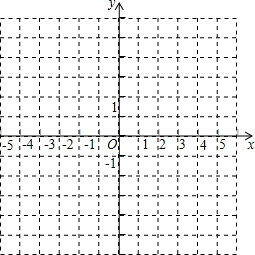 如图,在平面直角坐标系xOy中,A(-1.5),B(-1,0),C(-4,3),
如图,在平面直角坐标系xOy中,A(-1.5),B(-1,0),C(-4,3),