题目内容
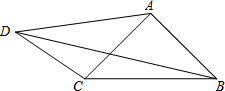 如图,在四边形ABCD中,AD=5,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD的长为( )
如图,在四边形ABCD中,AD=5,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
考点:勾股定理
专题:
分析:根据等式的性质,可得∠BAD与∠CAD′的关系,根据SAS,可得△BAD与△CAD′的关系,根据全等三角形的性质,可得BD与CD′的关系,根据勾股定理,可得答案.
解答:解:作AD′⊥AD,AD′=AD,连接CD′,DD′,如图: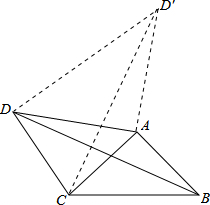
∵∠BAC+∠CAD=∠DAD′+∠CAD,
即∠BAD=∠CAD′,
在△BAD与△CAD′中,
,
∴△BAD≌△CAD′(SAS),
∴BD=CD′.
∠DAD′=90°
由勾股定理得DD′=
=5
,
∠D′DA+∠ADC=90°
由勾股定理得CD′=
=
,
∴BD=CD′=
,
故选:D.

∵∠BAC+∠CAD=∠DAD′+∠CAD,
即∠BAD=∠CAD′,
在△BAD与△CAD′中,
|
∴△BAD≌△CAD′(SAS),
∴BD=CD′.
∠DAD′=90°
由勾股定理得DD′=
| AD2+AD′2 |
| 2 |
∠D′DA+∠ADC=90°
由勾股定理得CD′=
| DC2+DD′2 |
| 32+50 |
∴BD=CD′=
| 59 |
故选:D.
点评:本题考查了全等三角形的判定与性质,利用了全等三角形的判定与性质,勾股定理,作出全等图形是解题关键.

练习册系列答案
相关题目
甲、乙、丙、丁四名射击运动员参加射击预选赛,他们射击成绩的平均环数
及方差S2如下表所示:
若要选出一个成绩较好且状态稳定的运动员去参赛,那么应选运动员( )
. |
| x |
| 甲 | 乙 | 丙 | 丁 | |||
| 8 | 9 | 9 | 8 | ||
| S2 | 1 | 1.1 | 1.2 | 1.3 |
| A、甲 | B、乙 | C、丙 | D、丁 |
若a、b互为相反数,c、d互为倒数,则a+b-cd的值是( )
| A、0 | B、1 | C、-1 | D、-2 |
满足下列条件,不能证明两个三角形全等的是( )
| A、AB=A′B′,∠A=∠A′,AC=A′C′ |
| B、∠A=∠A′,∠B=∠B′,AB=A′B′ |
| C、AB=A′B′,BC=B′C′,AC=A′C′ |
| D、AB=A′B′,∠B=∠B′,AC=A′C′ |
一元二次方程x2+3x=0的根是( )
| A、x=0或x=-3 |
| B、x=0或x=3 |
| C、x=0 |
| D、x=-3 |
 如图,△ABC中,∠C=90°,AC=BC=a,AB=b,AD平分∠CAB交BC于D,DE⊥AB,垂足为E,则△DEB的周长为
如图,△ABC中,∠C=90°,AC=BC=a,AB=b,AD平分∠CAB交BC于D,DE⊥AB,垂足为E,则△DEB的周长为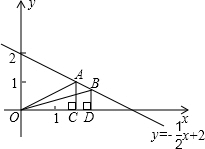 一次函数y=-
一次函数y=-