题目内容
13.用棋子摆出下列一组图形:
若照这样的方式摆下去,某一图形共有99枚棋子,则它是第32个图形.
分析 观察图形,发现图(1)中是6个棋子,图(2)中是6+3=9个棋子,图(3)中是9+3=12个棋子,…后边的图形比前面的图形依次多3个棋子.根据这一规律即可解决下列问题.
解答 解:由题意可得第n个图形棋子的枚数是6+3(n-1)=3n+3个.
99=3n+3,
解得n=32.
答:某一图形共有99枚棋子,它是第32个图形.
故答案为:32.
点评 此题考查图形的变化规律,从简单情形入手,找出图形之间的联系,得出运算的规律,利用规律解决问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.计算-3xy2+2xy2的结果是( )
| A. | -5xy2 | B. | -xy2 | C. | -x2y4 | D. | -5x2y4 |
8.已知B、C两点把线段AD分成2:3:4三部分,M是AD的中点,CD=12,则MC的长为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
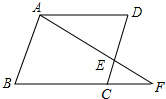 如图,在平行四边形ABCD中,F是BC延长线上一点,连接AF交CD于点E,若AB=a,AD=b,CE=m,求BF的长.
如图,在平行四边形ABCD中,F是BC延长线上一点,连接AF交CD于点E,若AB=a,AD=b,CE=m,求BF的长.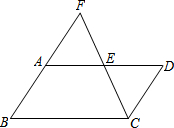 已知:如图,?ABCD中,点E是AD的中点,延长CE交BA的延长线于点F.猜想AB与AF有什么关系?为什么?
已知:如图,?ABCD中,点E是AD的中点,延长CE交BA的延长线于点F.猜想AB与AF有什么关系?为什么?