题目内容
9.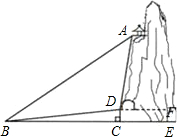 某景区有一个景观奇异的天门洞,D点是洞的入口,游人从入口进洞游览后,可经山洞到达山顶的出口凉亭A处观看旅游区风景,最后坐缆车沿索道AB返回山脚下的B处,在同一平面内,若测得斜坡BD的长为100米,坡角∠DBC=10°,在B处测得A的仰角∠ABC=40°,在D处测得A的仰角∠ADF=85°,过D点作地面BE的垂线,垂足为C.
某景区有一个景观奇异的天门洞,D点是洞的入口,游人从入口进洞游览后,可经山洞到达山顶的出口凉亭A处观看旅游区风景,最后坐缆车沿索道AB返回山脚下的B处,在同一平面内,若测得斜坡BD的长为100米,坡角∠DBC=10°,在B处测得A的仰角∠ABC=40°,在D处测得A的仰角∠ADF=85°,过D点作地面BE的垂线,垂足为C.(1)求∠ADB的度数;
(2)过D点作AB的垂线,垂足为G,求DG的长及索道AB的长.(结果保留根号)
分析 (1)利用点D处的周角即可求得∠ADB的度数;
(2)首先分析图形,根据题意构造直角三角形.本题涉及到两个直角三角形,应利用其公共边构造三角关系,进而可求出答案.
解答 解:(1)∵DC⊥CE,
∴∠BCD=90°,
又∵∠DBC=10°,
∴∠BDC=80°,
∵∠ADF=85°,
∴∠ADB=360°-80°-90°-85°=105°;
(2)过点D作DG⊥AB于点G.
在Rt△GDB中,
∠GBD=40°-10°=30°,
∴∠BDG=90°-30°=60°,
又∵BD=100,
∴GD=BD=100×$\frac{1}{2}$=50,
∴GB=BD×cos30°=100×$\frac{\sqrt{3}}{2}$=50$\sqrt{3}$,
在Rt△ADG=105°-60°=45°,
∴GD=GA=50,
∴AB=AG+GB=50+50$\sqrt{3}$,
答:索道长(50+50$\sqrt{3}$)米.
点评 本题考查仰角的定义及直角三角形的解法,首先构造直角三角形,再借助角边关系、三角函数的定义解题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.如果点P(a-4,a)在y轴上,则点P的坐标是( )
| A. | (4,0) | B. | (0,4) | C. | (-4,0) | D. | (0,-4) |
14.已知:顺次连接矩形各边的中点,得到一个菱形,如图1;再次顺次连接菱形各边的中点,得到一个新的矩形,如图2;然后顺次连接新的矩形各边的中点,得到一个新的菱形,如图3;如此反复操作下去,则第2 013个图形中直角三角形的个数有( )
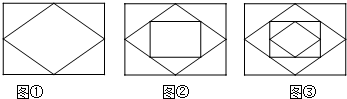

| A. | 4 028个 | B. | 4 024个 | C. | 4 022个 | D. | 2 012个 |
1.计算-3xy2+2xy2的结果是( )
| A. | -5xy2 | B. | -xy2 | C. | -x2y4 | D. | -5x2y4 |
 如图,我国一渔政船在钓鱼岛O正北方向、距钓鱼岛15海里的B处执法,发现在其南偏东60°的方向上有一不明国籍船只在钓鱼岛正东方向的点A处匀速向我国钓鱼岛驶进,我国渔政船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船.
如图,我国一渔政船在钓鱼岛O正北方向、距钓鱼岛15海里的B处执法,发现在其南偏东60°的方向上有一不明国籍船只在钓鱼岛正东方向的点A处匀速向我国钓鱼岛驶进,我国渔政船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船.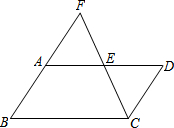 已知:如图,?ABCD中,点E是AD的中点,延长CE交BA的延长线于点F.猜想AB与AF有什么关系?为什么?
已知:如图,?ABCD中,点E是AD的中点,延长CE交BA的延长线于点F.猜想AB与AF有什么关系?为什么?