题目内容
5. 如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC 上,以AD为折痕△ABD折叠得到△AB′D,AB′与边BC交于点E.若△DEB′为直角三角形,则BD的长是2或5.
如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC 上,以AD为折痕△ABD折叠得到△AB′D,AB′与边BC交于点E.若△DEB′为直角三角形,则BD的长是2或5.
分析 先依据勾股定理求得AB的长,然后由翻折的性质可知:AB′=10,DB=DB′,接下来分为∠B′DE=90°和∠B′ED=90°,两种情况画出图形,设DB=DB′=x,然后依据勾股定理列出关于x的方程求解即可.
解答 解:∵Rt△ABC纸片中,∠C=90°,AC=6,BC=8,
∴AB=10,
∵以AD为折痕△ABD折叠得到△AB′D,
∴BD=DB′,AB′=AB=10.
如图1所示:当∠B′DE=90°时,过点B′作B′F⊥AF,垂足为F.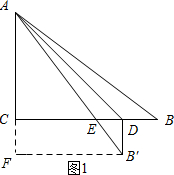
设BD=DB′=x,则AF=6+x,FB′=8-x.
在Rt△AFB′中,由勾股定理得:AB′2=AF2+FB′2,即(6+x)2+(8-x)2=102.
解得:x1=2,x2=0(舍去).
∴BD=2.
如图2所示:当∠B′ED=90°时,C与点E重合.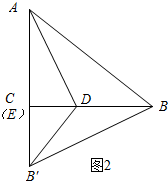
∵AB′=10,AC=6,
∴B′E=4.
设BD=DB′=x,则CD=8-x.
在Rt△′BDE中,DB′2=DE2+B′E2,即x2=(8-x)2+42.
解得:x=5.
∴BD=5.
综上所述,BD的长为2或5.
故答案为:2或5.
点评 本题主要考查的是翻折的性质、勾股定理的应用,根据勾股定理列出关于x的方程是解题的关键.

练习册系列答案
相关题目
19.已知一组数据0,-1,1,2,3,则这组数据的方差为( )
| A. | 1 | B. | -1 | C. | $\sqrt{2}$ | D. | 2 |
10.已知函数y=ax2-2ax-1(a是常数,a≠0),下列结论正确的是( )
| A. | 当a=1时,函数图象过点(-1,1) | |
| B. | 当a=-2时,函数图象与x轴没有交点 | |
| C. | 若a>0,则当x≥1时,y随x的增大而减小 | |
| D. | 若a<0,则当x≤1时,y随x的增大而增大 |
16.分别取正整数5的绝对值、倒数、相反数、算术平方根,得到的数值仍为正整数的是( )
| A. | 绝对值 | B. | 倒数 | C. | 相反数 | D. | 算术平方根 |
13. 如图的矩形ABCD中,E点在CD上,且AE<AC.若P、Q两点分别在AD、AE上,AP:PD=4:1,AQ:QE=4:1,直线PQ交AC于R点,且Q、R两点到CD的距离分别为q、r,则下列关系何者正确?( )
如图的矩形ABCD中,E点在CD上,且AE<AC.若P、Q两点分别在AD、AE上,AP:PD=4:1,AQ:QE=4:1,直线PQ交AC于R点,且Q、R两点到CD的距离分别为q、r,则下列关系何者正确?( )
 如图的矩形ABCD中,E点在CD上,且AE<AC.若P、Q两点分别在AD、AE上,AP:PD=4:1,AQ:QE=4:1,直线PQ交AC于R点,且Q、R两点到CD的距离分别为q、r,则下列关系何者正确?( )
如图的矩形ABCD中,E点在CD上,且AE<AC.若P、Q两点分别在AD、AE上,AP:PD=4:1,AQ:QE=4:1,直线PQ交AC于R点,且Q、R两点到CD的距离分别为q、r,则下列关系何者正确?( )| A. | q<r,QE=RC | B. | q<r,QE<RC | C. | q=r,QE=RC | D. | q=r,QE<RC |
13.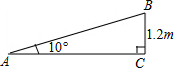 一个公共房门前的台阶高出地面1.2米,台阶拆除后,换成供轮椅行走的斜坡,数据如图所示,则下列关系或说法正确的是( )
一个公共房门前的台阶高出地面1.2米,台阶拆除后,换成供轮椅行走的斜坡,数据如图所示,则下列关系或说法正确的是( )
 一个公共房门前的台阶高出地面1.2米,台阶拆除后,换成供轮椅行走的斜坡,数据如图所示,则下列关系或说法正确的是( )
一个公共房门前的台阶高出地面1.2米,台阶拆除后,换成供轮椅行走的斜坡,数据如图所示,则下列关系或说法正确的是( )| A. | 斜坡AB的坡度是10° | B. | 斜坡AB的坡度是tan10° | ||
| C. | AC=1.2tan10°米 | D. | AB=$\frac{1.2}{cos10°}$米 |
 如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C6,若点P(11,m)在第6段抛物线C6上,则m=-1.
如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C6,若点P(11,m)在第6段抛物线C6上,则m=-1.