题目内容
若ax2+bx+c﹙a、b、c是常数﹚是完全平方式．求证：b2-4ac=0．
考点：完全平方式
专题：证明题
分析：先设ax2+bx+c=（mx+n）2，m，n是常数再根据完全平方公式计算，根据恒等式的性质 得：b2-4ac=（2mn）2-4m2n2=0．
解答：证明：设ax2+bx+c=（mx+n）2，m，n是常数
那么：ax2+bx+c=m2x2+2mnx+n2
根据恒等式的性质 得：b2-4ac=（2mn）2-4m2n2=0．
那么：ax2+bx+c=m2x2+2mnx+n2
根据恒等式的性质 得：b2-4ac=（2mn）2-4m2n2=0．
点评：本题是完全平方公式的应用；两数的平方和，再加上或减去它们积的2倍，就构成了一个完全平方式．本题关键是设设ax2+bx+c=（mx+n）2，m，n是常数．
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
矩形的周长是16cm，设矩形的一边长为xcm，另一边长为ycm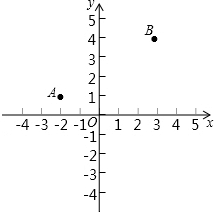
如图，点A、B在平面直角坐标系的x轴的上方，其坐标为A（-2，1）、B（3，4）．
如图，在△ABC中，∠C=90°，AC=BC，BD平分∠ABC，DE⊥AB于点E，若△BCD与△ABC的面积之比是3：8，求△ADE与△ABC的面积之比．