题目内容
7.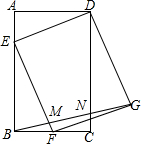 如图,在矩形ABCD中,AB=3,BC=2,点F是BC的中点,点E是边AB上一点,且BE=2,连结DE,EF,并以DE,EF为边作?EFGD,连结BG,分别交EF和DC于点M,N,则$\frac{BM}{NG}$=$\frac{6}{7}$.
如图,在矩形ABCD中,AB=3,BC=2,点F是BC的中点,点E是边AB上一点,且BE=2,连结DE,EF,并以DE,EF为边作?EFGD,连结BG,分别交EF和DC于点M,N,则$\frac{BM}{NG}$=$\frac{6}{7}$.
分析 先判定四边形DEFG是正方形,进而得出∠EFG=90°,DG=DE=FG=$\sqrt{5}$,过B作BH⊥EF于H,根据勾股定理以及相似三角形的性质,求得EM的长,再根据∠EBM=∠DNG,∠EMB=∠DGN,即可判定△EBM∽△DNG,进而得到$\frac{BM}{NG}$=$\frac{EM}{DG}$=$\frac{6}{7}$.
解答 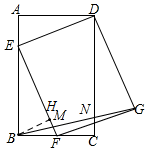 解:∵矩形ABCD中,AB=3,BC=2,点F是BC的中点,
解:∵矩形ABCD中,AB=3,BC=2,点F是BC的中点,
∴BF=1,AD=2,
又∵BE=2,
∴AE=BF=1,DE=$\sqrt{5}$=FG,
又∵∠A=∠EBF=90°,
∴△ADE≌△BEF,
∴∠ADE=∠BEF,DE=EF,
又∵∠ADE+∠AED=90°,
∴∠BEF+∠AED=90°,
∴∠DEF=90°,
∴四边形DEFG是正方形,
∴∠EFG=90°,DG=DE=$\sqrt{5}$,
如图,过B作BH⊥EF于H,
∵Rt△ABF中,EF=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∴BH=$\frac{BF×BE}{EF}$=$\frac{2}{5}\sqrt{5}$,
∴Rt△BFH中,HF=$\sqrt{B{F}^{2}-B{H}^{2}}$=$\frac{\sqrt{5}}{5}$,
∵BH∥FG,
∴△BHM∽△GFM,
∴$\frac{HM}{FM}$=$\frac{BH}{GF}$=$\frac{\frac{2}{5}\sqrt{5}}{\sqrt{5}}$=$\frac{2}{5}$,
∴FM=$\frac{5}{7}$×FH=$\frac{\sqrt{5}}{7}$,
∴EM=EF-FM=$\sqrt{5}$-$\frac{\sqrt{5}}{7}$=$\frac{6}{7}\sqrt{5}$,
∵EB∥DN,EM∥DG,
∴∠EBM=∠DNG,∠EMB=∠DGN,
∴△EBM∽△DNG,
∴$\frac{BM}{NG}$=$\frac{EM}{DG}$=$\frac{\frac{6}{7}\sqrt{5}}{\sqrt{5}}$=$\frac{6}{7}$.
故答案为:$\frac{6}{7}$.
点评 本题主要考查了相似三角形的判定与性质,平行四边形的性质,矩形的性质以及正方形的判定的综合应用,解决问题的关键是作辅助线,构造相似三角形和直角三角形,依据勾股定理以及相似三角形的对应边成比例进行计算求解.

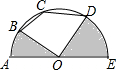 如图,半圆O的直径AE=8,点B,C,D均在半圆上,若AB=BC,CD=DE,连接OB,OD,则图中阴影部分的面积为( )
如图,半圆O的直径AE=8,点B,C,D均在半圆上,若AB=BC,CD=DE,连接OB,OD,则图中阴影部分的面积为( )| A. | 2π | B. | 4π | C. | 8π | D. | 16π |

| 价格类型 | A型 | B型 |
| 进价(元/件) | 60 | 100 |
| 标价(元/件) | 100 | 160 |


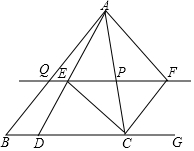 如图,在△ABC 中,点P是AC边上的一点,过点P作与BC平行的直线PQ,交AB于点Q,点D在线段 BC上,联接AD交线段PQ于点E,且$\frac{CP}{CD}$=$\frac{QE}{BD}$,点G在BC延长线上,∠ACG的平分线交直线PQ于点F.
如图,在△ABC 中,点P是AC边上的一点,过点P作与BC平行的直线PQ,交AB于点Q,点D在线段 BC上,联接AD交线段PQ于点E,且$\frac{CP}{CD}$=$\frac{QE}{BD}$,点G在BC延长线上,∠ACG的平分线交直线PQ于点F.