题目内容
11.一次函数y1=-x+2,反比例函数y2=$-\frac{8}{x}$,当y1<y2时,x的取值范围-2<x<0或x>4.分析 求出两个函数的交点坐标,再画出两个函数的草图,根据图象和交点坐标即可得出答案.
解答  解:将一次函数y1=-x+2与反比例函数y2=$-\frac{8}{x}$组成方程组得,
解:将一次函数y1=-x+2与反比例函数y2=$-\frac{8}{x}$组成方程组得,
$\left\{\begin{array}{l}{y=-x+2}\\{y=-\frac{8}{x}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-2}\\{y=4}\end{array}\right.$或$\left\{\begin{array}{l}{x=4}\\{y=-2}\end{array}\right.$.
则两交点坐标为(-2,4),(4,-2).
如图:当y1<y2时,x的取值范围是-2<x<0或x>4.
故答案为-2<x<0或x>4;
点评 本题考查了反比例函数与一次函数的交点问题,求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了数形结合的思想.

练习册系列答案
相关题目
19.某服装店用6000元购进A,B两种新式服装,按标价售出后可获得毛利润3800元(毛利润=售价-进价),这两种服装的进价、标价如表所示:
求这两种服装各购进的件数.
| 价格类型 | A型 | B型 |
| 进价(元/件) | 60 | 100 |
| 标价(元/件) | 100 | 160 |
1.下列方程中,是二元一次方程的是( )
| A. | 2x2-3y=12 | B. | 4x-4y=7 | C. | $\frac{1}{x}$-y-2=0 | D. | x-y+xy=6 |

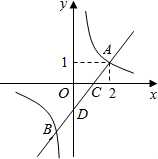 如图,一次函数y=x+m的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
如图,一次函数y=x+m的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1). 如图,直线AC∥BD,BC平分∠ABD,DE⊥BC,∠MAB=80°,求∠EDB的度数.
如图,直线AC∥BD,BC平分∠ABD,DE⊥BC,∠MAB=80°,求∠EDB的度数.