题目内容
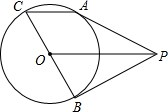 如图所示,BC是⊙O的直径,P为⊙O外的一点,PA、PB为⊙O的切线,切点分别为A、B.试证明:AC∥OP.
如图所示,BC是⊙O的直径,P为⊙O外的一点,PA、PB为⊙O的切线,切点分别为A、B.试证明:AC∥OP.考点:切线的性质
专题:证明题
分析:连接AB交PO于F,根据切线的性质得到PO垂直平分AB,再根据直径所对的圆周角是直角可得∠CAB=90°,于是∠CAB=∠OFB,所以AC∥OP.
解答: 证明:连接AB交OP于F,连接AO.
证明:连接AB交OP于F,连接AO.
∵PA,PB是圆的切线,
∴PA=PB,
∵OA=OB
∴PO垂直平分AB.
∴∠OFB=90°.
∵BC是直径,
∴∠CAB=90°.
∴∠CAB=∠OFB.
∴AC∥OP.
 证明:连接AB交OP于F,连接AO.
证明:连接AB交OP于F,连接AO.∵PA,PB是圆的切线,
∴PA=PB,
∵OA=OB
∴PO垂直平分AB.
∴∠OFB=90°.
∵BC是直径,
∴∠CAB=90°.
∴∠CAB=∠OFB.
∴AC∥OP.
点评:本题考查了切线的性质、圆周角定理在圆中:直径所对的圆周角是直角.

练习册系列答案
相关题目
在代数式中2x3,-ab2,13xyz,8πr2是三次单项式的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
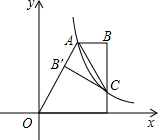 如图,双曲线y=
如图,双曲线y=