Question

14．叙述三角形内角和定理并将证明过程填写完整．
定理：三角形内角和是180°．
已知：△ABC．求证：∠A+∠B+∠C=180°．
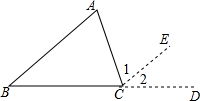
证明：作边BC的延长线CD，过C点作CE∥AB．
∴∠1=∠A两直线平行，内错角相等，
∠2=∠B两直线平行，同位角相等，
∵∠ACB+∠1+∠2=180°平角的定义，
∴∠A+∠B+∠ACB=180°等量代换．

Answer 1

分析 延长BC到D，过点C作CE∥BA，根据两直线平行，同位角相等可得∠B=∠1，两直线平行，内错角相等可得∠A=∠2，再根据平角的定义列式整理即可得证．

解答 证明：如图，延长BC到D，过点C作CE∥BA，
∵BA∥CE，
∴∠A=∠1（两直线平行，内错角相等），
∠B=∠2（两直线平行，同位角相等），
又∵∠BCD=∠BCA+∠2+∠1=180°（平角的定义），
∴∠A+∠B+∠ACB=180°（等量代换）．
故答案为：两直线平行，内错角相等．两直线平行，同位角相等，平角的定义，等量代换．

点评 本题考查了三角形的内角和定理的证明，作辅助线把三角形的三个内角转化到一个平角上是解题的关键．