题目内容
9.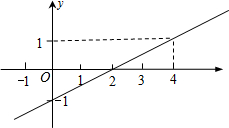 已知一次函数y=$\frac{1}{2}$x-1的图象如图所示,下列正确的有( )个.
已知一次函数y=$\frac{1}{2}$x-1的图象如图所示,下列正确的有( )个.①点(-2,-3)在该函数的图象上
②方程$\frac{1}{2}$x-1=0的解为x=2
③当x>2时,y的取值范围是y>0
④该直线与直线y=-1+3x平行.
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 ①把x=-2代入解析式求得函数值与-3比较即可判断;②由图象与x轴的交点即可判定;③根据图象即可判断;④用两直线的系数k的值来判定即可.
解答 解:把x=-2代入解析式求得y=-2≠-3,所以①错误;
∵直线y=$\frac{1}{2}$x-1与x轴的交点为(2,0),
∴方程$\frac{1}{2}$x-1=0的解为x=2,所以②正确;
由图象可知,当x>2时,y>0,所以③正确;
∵直线y=$\frac{1}{2}$x-1的一次项系数与直线y=-1+3x的一次项系数不等,所以直线y=$\frac{1}{2}$x-1直线y=-1+3x不平行,所以④错误,
故选A.
点评 本题考查了一次函数图象上点的坐标特征,一次函数和一元一次方程以及不等式的关系,两条直线平行问题等,利用数形结合求解是解答此题的关键.

练习册系列答案
相关题目
17. 如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=( )
如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=( )
 如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=( )
如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=( )| A. | 60° | B. | 55° | C. | 50° | D. | 无法计算 |
14.已知关于x的一元二次方程x2+bx+a=0有一个非零根-a,则a-b的值为( )
| A. | 1 | B. | -1 | C. | 0 | D. | -2 |
 已知线段a、b,用圆规和直尺画线段AC,使它等于AC=2a+b.(保留作图痕迹,并写出简要作法)
已知线段a、b,用圆规和直尺画线段AC,使它等于AC=2a+b.(保留作图痕迹,并写出简要作法)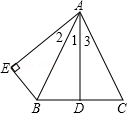 已知:如图,AB=AC,点D是BC的中点,AB平分∠DAE,AE⊥BE,垂足为E.
已知:如图,AB=AC,点D是BC的中点,AB平分∠DAE,AE⊥BE,垂足为E.