题目内容
如图,在四边形ABCD中,AD∥BC,AD=BC,求证:AB∥CD.
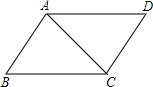

考点:全等三角形的判定与性质
专题:
分析:根据平行线的性质得出∠DAC=∠ACB,SAS求出△DAC≌△BCA,推出∠DCA=∠BAC,即可得出答案.
解答:证明:∵AD∥BC,
∴∠DAC=∠ACB,
在△DAC和△BCA中,
,
∴△DAC≌△BCA(SAS),
∴∠DCA=∠BAC,
∴AB∥CD.
∴∠DAC=∠ACB,
在△DAC和△BCA中,
|
∴△DAC≌△BCA(SAS),
∴∠DCA=∠BAC,
∴AB∥CD.
点评:本题考查了全等三角形的性质和判定,平行线的性质和判定的应用,主要考查学生的推理能力.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 如图,两个同心圆的圆心为O,矩形ABCD的边AB为大圆的弦,边DC与小圆相切于点E,连接OE并延长交AB于点F.已知OA=4,AF=2.
如图,两个同心圆的圆心为O,矩形ABCD的边AB为大圆的弦,边DC与小圆相切于点E,连接OE并延长交AB于点F.已知OA=4,AF=2.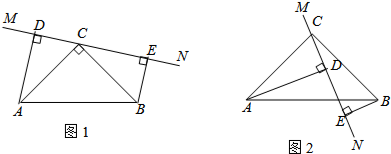
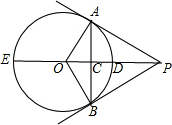 如图,PA、PB是⊙O的切线,切点分别为A、B,直线OP交⊙O于点D、E,交AB于点C.
如图,PA、PB是⊙O的切线,切点分别为A、B,直线OP交⊙O于点D、E,交AB于点C. 如图,在△ABC中,两条中线AD、BE交于点F,则S△EDF:S△ABC=
如图,在△ABC中,两条中线AD、BE交于点F,则S△EDF:S△ABC= 如图,一个圆柱,它的高为20cm,底面半径为7cm.如果一只蚂蚁要自圆柱下底面的A点,沿圆柱体的侧面爬到与A相对的上底面B点,求爬行的最短长度(结果保留π).
如图,一个圆柱,它的高为20cm,底面半径为7cm.如果一只蚂蚁要自圆柱下底面的A点,沿圆柱体的侧面爬到与A相对的上底面B点,求爬行的最短长度(结果保留π).