题目内容
2.(1)已知xy=8,x2+y2=2,求(x+y)2+4xy的值;(2)先化简,再求值:[x(x2y2-xy)-y(x2-x2y)]÷3x2y,其中x=1,y=3.
分析 (1)根据完全平方公式进行化简即可求出答案.
(2)先将原式进行化简,然后将x=1和y=3代入即可求出答案.
解答 解:(1)∵xy=8,x2+y2=2,
∴原式=x2+2xy+y2+4xy
=x2+y2+6xy
=2+48
=50
(2)当x=1,y=3时,
原式=(x3y2-x2y-x2y+x2y2)÷3x2y
=(x3y2-2x2y+x2y2)÷3x2y
=$\frac{1}{3}$xy-$\frac{2}{3}$+$\frac{1}{3}$y
=1-$\frac{2}{3}$+1
=$\frac{4}{3}$
点评 本题考查整式运算,解题的关键是熟练运用整式的运算法则,本题属于基础题型.

练习册系列答案
相关题目
12.如图所示的立体图形中,含有曲面的是( )


| A. | (1)(2) | B. | (1)(3) | C. | (2)(3) | D. | (2)(4) |
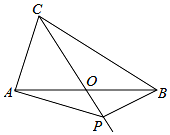 如图,在△ABC中,AB=BC=6,AO=BO,P是射线CO上在AB下方的一个动点,∠AOC=45°.则当△PAB为直角三角形时,AP的长为$\sqrt{18+9\sqrt{2}}$或=$\sqrt{18-9\sqrt{2}}$或3$\sqrt{5}$.
如图,在△ABC中,AB=BC=6,AO=BO,P是射线CO上在AB下方的一个动点,∠AOC=45°.则当△PAB为直角三角形时,AP的长为$\sqrt{18+9\sqrt{2}}$或=$\sqrt{18-9\sqrt{2}}$或3$\sqrt{5}$.
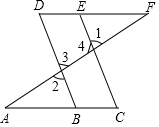 如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,求证DF∥AC.
如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,求证DF∥AC.