题目内容
11.下列计算正确的是( )| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | $\sqrt{12}$-$\sqrt{3}$=$\sqrt{3}$ | C. | $\sqrt{8}$÷$\sqrt{2}$=4 | D. | $\sqrt{(-5)^{2}}$=-5 |
分析 根据二次根式的加减法则对各选项进行逐一分析即可.
解答 解:A、$\sqrt{2}$与$\sqrt{3}$不是同类项,不能合并,故本选项错误;
B、$\sqrt{12}$-$\sqrt{3}$=2$\sqrt{3}$-$\sqrt{3}$=$\sqrt{3}$,故本选项正确;
C、$\sqrt{8}$÷$\sqrt{2}$=$\sqrt{\frac{8}{2}}$=$\sqrt{4}$=2≠4,故本选项错误;
D、($\sqrt{(-5)^{2}}$)=5≠-5,故本选项错误.
故选B.
点评 本题考查的是二次根式的加减法,熟知二次根式相加减,先把各个二次根式化成最简二次根式,再把被开方数相同的二次根式进行合并,合并方法为系数相加减,根式不变是解答此题的关键.

练习册系列答案
相关题目
20.一个口袋中装有12个乒乓球,其中3个球涂成黄色,5个球涂成绿色,4个球涂成红色.从中任意摸出一个乒乓球,这个球是红色的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
1.经检测,外观和质地相同的一种产品,不合格产品的概率是$\frac{2}{15}$.某单位买了这样的产品60件,则所买产品中合格产品的件数为( )
| A. | 8件 | B. | 16件 | C. | 44件 | D. | 52件 |
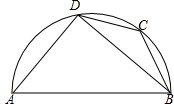 如图,AB是半圆的直径,AD是半圆的弦,C是$\widehat{BD}$的中点,∠BAD=50°,求∠ABC的度数.
如图,AB是半圆的直径,AD是半圆的弦,C是$\widehat{BD}$的中点,∠BAD=50°,求∠ABC的度数. 如图,已知△ABC中,∠ABC的平分线与外角∠ACD的平分线相交于点I,∠A与∠BIC之间有怎样的数量关系?请说明理由.
如图,已知△ABC中,∠ABC的平分线与外角∠ACD的平分线相交于点I,∠A与∠BIC之间有怎样的数量关系?请说明理由.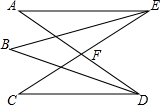 如图,EC与AD相交于F,EB、DB平分∠AEC、∠ADC交于点B.
如图,EC与AD相交于F,EB、DB平分∠AEC、∠ADC交于点B.