题目内容
8.在Rt△ABC中,AC=BC=4,⊙C与直线AB相切,则⊙C的半径为( )| A. | 2 | B. | 4 | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
分析 首先根据题意画出图形,然后设切点为D,连接CD,根据切线的性质与等腰直角三角形的性质,可求得⊙C的半径.
解答  解:如图,设切点为D,连接CD,
解:如图,设切点为D,连接CD,
∵⊙C与直线AB相切,
∴CD⊥AB,
∵在Rt△ABC中,AC=BC=4,
∴AB=4$\sqrt{2}$,AD=BD,
∴CD=$\frac{1}{2}$AB=2$\sqrt{2}$,
∴⊙C的半径为:2$\sqrt{2}$,
故选C.
点评 此题考查了切线的性质以及等腰直角三角形性质,熟练掌握切线的性质是解题的关键.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
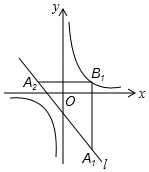 如图,在平面直角坐标系中,已知直线l:y=-x-1,双曲线y=$\frac{1}{x}$.在直线l上取点A1,过点A1作x轴的垂线交双曲线于点B1,过点B1作y轴的垂线交直线l于点A2,继续操作:过点A2作x轴的垂线交双曲线于点B2,过点B2作y轴的垂线交直线l于点A3,…,依次这样得到双曲线上的点B1,B2,B3,B4,…,Bn.记点A1的横坐标为2,则B2016的坐标为(-$\frac{1}{3}$,-3).
如图,在平面直角坐标系中,已知直线l:y=-x-1,双曲线y=$\frac{1}{x}$.在直线l上取点A1,过点A1作x轴的垂线交双曲线于点B1,过点B1作y轴的垂线交直线l于点A2,继续操作:过点A2作x轴的垂线交双曲线于点B2,过点B2作y轴的垂线交直线l于点A3,…,依次这样得到双曲线上的点B1,B2,B3,B4,…,Bn.记点A1的横坐标为2,则B2016的坐标为(-$\frac{1}{3}$,-3).