题目内容
3.解方程:(1)x(x+4)=-5(x+4)
(2)2x2-4x-9=0(用配方法解)
分析 (1)先提取公因式(x+4)得到(x+5)(x+4)=0,再解两个一元一次方程即可;
(2)先把二次项系数化为1,再进行配方,进而开方求出方程的解.
解答 解:(1)∵x(x+4)=-5(x+4),
∴(x+5)(x+4)=0,
∴x+5=0或x+4=0,
∴x1=-5,x2=-4;
(2)∵2x2-4x-9=0,
∴x2-2x-$\frac{9}{2}$=0,
∴(x2-2x+1)-1-$\frac{9}{2}$=0,
∴(x-1)2=$\frac{11}{2}$,
∴x-1=±$\frac{\sqrt{22}}{2}$,
∴x1=1+$\frac{\sqrt{22}}{2}$,x2=1-$\frac{\sqrt{22}}{2}$.
点评 本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
8.在Rt△ABC中,AC=BC=4,⊙C与直线AB相切,则⊙C的半径为( )
| A. | 2 | B. | 4 | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
18.如果a表示一个负数,则|a|等于( )
| A. | a | B. | 0 | C. | -a | D. | 不确定 |
 如图,已知△ABC和△ADE是等边三角形,联结BD、CE.
如图,已知△ABC和△ADE是等边三角形,联结BD、CE.
 如图,将长方形ABCD沿AE折叠,使点D落在BC边上的点F,若∠FEC=56°,则∠AED=62°.
如图,将长方形ABCD沿AE折叠,使点D落在BC边上的点F,若∠FEC=56°,则∠AED=62°.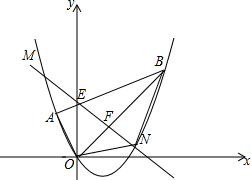 如图,平面直角坐标系xOy中点A的坐标为(-1,1),点B的坐标为(3,3),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点E.
如图,平面直角坐标系xOy中点A的坐标为(-1,1),点B的坐标为(3,3),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点E. 如图是按规律排列的式子,若第六行最中间两项的和的值是2052,则a的值为±2.
如图是按规律排列的式子,若第六行最中间两项的和的值是2052,则a的值为±2. 甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距80千米的B地,行驶过程中的函数图象如图所示,请根据图象回答下列问题:
甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距80千米的B地,行驶过程中的函数图象如图所示,请根据图象回答下列问题: