题目内容
15.式子(1+$\frac{1}{3}$)(1+$\frac{1}{{3}^{2}}$)(1+$\frac{1}{{3}^{4}}$)(1+$\frac{1}{{3}^{8}}$)计算结果正确的是( )| A. | $\frac{1}{2}$×(1-$\frac{1}{{3}^{16}}$) | B. | 1-$\frac{1}{{3}^{16}}$ | C. | $\frac{3}{2}$×(1-$\frac{1}{{3}^{16}}$) | D. | 3×(1-$\frac{1}{{3}^{16}}$) |
分析 求出式子(1-$\frac{1}{3}$)(1+$\frac{1}{3}$)(1+$\frac{1}{{3}^{2}}$)(1+$\frac{1}{{3}^{4}}$)(1+$\frac{1}{{3}^{8}}$)的结果是多少,即可求出式子(1+$\frac{1}{3}$)(1+$\frac{1}{{3}^{2}}$)(1+$\frac{1}{{3}^{4}}$)(1+$\frac{1}{{3}^{8}}$)的结果是多少.
解答 解:(1-$\frac{1}{3}$)(1+$\frac{1}{3}$)(1+$\frac{1}{{3}^{2}}$)(1+$\frac{1}{{3}^{4}}$)(1+$\frac{1}{{3}^{8}}$)
=(1-$\frac{1}{{3}^{2}}$)(1+$\frac{1}{{3}^{2}}$)(1+$\frac{1}{{3}^{4}}$)(1+$\frac{1}{{3}^{8}}$)
=(1-$\frac{1}{{3}^{4}}$)(1+$\frac{1}{{3}^{4}}$)(1+$\frac{1}{{3}^{8}}$)
=(1-$\frac{1}{{3}^{8}}$)(1+$\frac{1}{{3}^{8}}$)
=1-$\frac{1}{{3}^{16}}$
∴(1+$\frac{1}{3}$)(1+$\frac{1}{{3}^{2}}$)(1+$\frac{1}{{3}^{4}}$)(1+$\frac{1}{{3}^{8}}$)
=(1-$\frac{1}{{3}^{16}}$)÷(1-$\frac{1}{3}$)
=$\frac{3}{2}$×(1-$\frac{1}{{3}^{16}}$)
故选:C.
点评 此题主要考查了有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.

 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案| A. | 2.6×105 | B. | 26×104 | C. | 2.6×104 | D. | 0.26×106 |
| A. | 49(1-x)2=49-25 | B. | 49(1-2x)=25 | C. | 49(1-x)2=25 | D. | 49(1-x2)=25 |
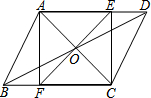 在?ABCD中,对角线AC、BD相交于O,EF过点O,且AF⊥BC.
在?ABCD中,对角线AC、BD相交于O,EF过点O,且AF⊥BC.