题目内容
16.矩形的两条对角线的夹角为60°,较短的边长为2cm,则较长的边长为2$\sqrt{3}$cm.分析 如图,首先证明△AOB是等边三角形,求出AC,在Rt△ABC中,利用勾股定理即可解决问题.
解答 解:如图,
∵四边形ABCD是矩形,
∴OA=OC=OB=OD,∠ABC=90°,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴OA=OB=AB=2,AC=2OA=4,
在Rt△ABC中,BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$.
故答案为2$\sqrt{3}$
点评 本题考查矩形的性质、等边三角形的判定和性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
11.已知x≠0且M=(x2+2x+1)(x2-2x+1),N=(x2+x+1)(x2-x+1),则M与N的大小关系为( )
| A. | M>N | B. | M=N | C. | M<N | D. | 无法确定 |
8.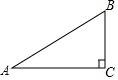 如图,在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA的值是( )
如图,在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA的值是( )
 如图,在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA的值是( )
如图,在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA的值是( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{\sqrt{7}}{4}$ | D. | $\frac{4}{5}$ |
 如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E,AE=2,CE=1.
如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E,AE=2,CE=1.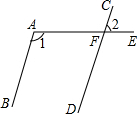 如图,AB∥CD,射线AE交CD于点F,若∠1=115°,则∠2的度数是65°.
如图,AB∥CD,射线AE交CD于点F,若∠1=115°,则∠2的度数是65°. 如图,在等边△ABC中,AB=4,P、M、N分别是BC、CA、AB边上动点,则PM+MN的最小值是2$\sqrt{3}$.
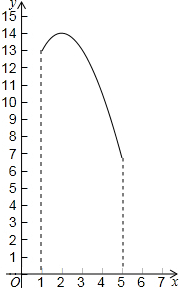
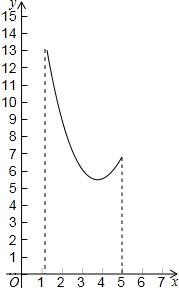
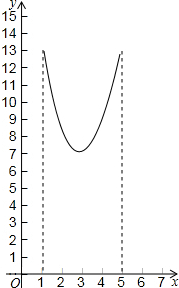
如图,在等边△ABC中,AB=4,P、M、N分别是BC、CA、AB边上动点,则PM+MN的最小值是2$\sqrt{3}$.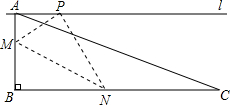 如图,在三角形纸片ABC中,∠ABC=90°,AB=5,BC=13,过点A,作直线l∥BC,折叠三角形纸片ABC,使点B落在直线l上的P处,折痕为MN.当点P在直线l上移动时,折痕的端点M、N也随之移动.若限定端点M、N分别在AB、BC边上移动,若设AP的长为x,MN的长为y,则下列选项,能表示y与x之间的函数关系的大致图象是( )
如图,在三角形纸片ABC中,∠ABC=90°,AB=5,BC=13,过点A,作直线l∥BC,折叠三角形纸片ABC,使点B落在直线l上的P处,折痕为MN.当点P在直线l上移动时,折痕的端点M、N也随之移动.若限定端点M、N分别在AB、BC边上移动,若设AP的长为x,MN的长为y,则下列选项,能表示y与x之间的函数关系的大致图象是( )