题目内容
10.应用无刻度的直尺画图:
在下面的三个图中,以OA为边,在正方形网格内作∠AOB=α,B点为格点(每个小正方形的顶点)使sinα的值分别为:$\frac{\sqrt{2}}{2}$,$\frac{3}{5}$和$\frac{\sqrt{10}}{10}$.
分析 如图(1)直角边长是5和5的直角三角形的斜边长是5$\sqrt{2}$,则sinα=$\frac{\sqrt{2}}{2}$,如图(2)直角边长是4和3的直角三角形的斜边长是5,则sinα=$\frac{3}{5}$;如图(3)直角边长是1和3的直角三角形的斜边长是$\sqrt{10}$,则sinα=$\frac{\sqrt{10}}{10}$.
解答 解:∠AOB为所求;
点评 本题考查的是勾股定理,锐角三角函数的定义,熟知在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边是解答此题的关键.

练习册系列答案
相关题目
18. 如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠B=68°,则∠BDC=( )
如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠B=68°,则∠BDC=( )
 如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠B=68°,则∠BDC=( )
如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠B=68°,则∠BDC=( )| A. | 44° | B. | 60° | C. | 67° | D. | 77° |
2.如图1,有两个全等的正三角形ABC和ODE,点O、C分别为△ABC、△ODE的重心;固定点O,将△ODE顺时针旋转,使得OD经过点C,如图2所示,则图2中四边形OGCF与△OCH面积的比为( )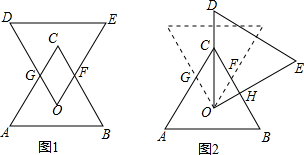

| A. | 1:1 | B. | 2:1 | C. | 4:1 | D. | 4:3 |
19.化简$\frac{{x}^{2}}{x-1}$+$\frac{x}{1-x}$的结果是( )
| A. | x+2 | B. | x-1 | C. | -x | D. | x |
 如图,直线AB、CD被直线EF所截,当满足条件∠1=∠5时(只需写出一个你认为合适的条件),AB∥CD.
如图,直线AB、CD被直线EF所截,当满足条件∠1=∠5时(只需写出一个你认为合适的条件),AB∥CD.