题目内容
15.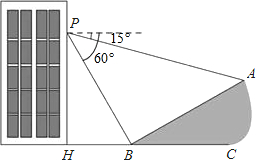 如图,小明在大楼30米高(即PH=30米)窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:$\sqrt{3}$,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC.求A、B两点间的距离.(结果精确到1米,参考数据:$\sqrt{3}$≈1.732).
如图,小明在大楼30米高(即PH=30米)窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:$\sqrt{3}$,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC.求A、B两点间的距离.(结果精确到1米,参考数据:$\sqrt{3}$≈1.732).
分析 首先根据题意得出∠ABF=30°,进而得出∠PBA=90°,∠BAP=45°,再利用锐角三角函数关系求出即可.
解答 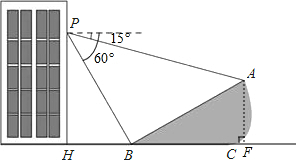 解:如图所示:过点A作AF⊥BC于点F,
解:如图所示:过点A作AF⊥BC于点F,
∵山坡的坡度i(即tan∠ABC)为1:$\sqrt{3}$,
∴tan∠ABF=$\frac{AF}{BF}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠ABF=30°,
∵在窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,
∴∠HPB=30°,∠APB=45°,
∴∠HBP=60°,
∴∠PBA=90°,∠BAP=45°,
∴PB=AB,
∵PH=30m,sin60°=$\frac{PH}{PB}$=$\frac{30}{PB}$=$\frac{\sqrt{3}}{2}$,
解得:PB=20$\sqrt{3}$,
故AB=20$\sqrt{3}$≈35(m),
答:A、B两点间的距离为35m.
点评 此题主要考查了解直角三角形的应用,正确得出PB=AB是解题关键.

练习册系列答案
相关题目
5.在2,-2,0,-3中,最大的数是( )
| A. | 2 | B. | -2 | C. | 0 | D. | -3 |
6.数据9、9、6、3、6、2、6的众数是( )
| A. | 2 | B. | 3 | C. | 6 | D. | 9 |
3. 如图,线段DE是△ABC的中位线,∠B=60°,则∠ADE的度数为( )
如图,线段DE是△ABC的中位线,∠B=60°,则∠ADE的度数为( )
 如图,线段DE是△ABC的中位线,∠B=60°,则∠ADE的度数为( )
如图,线段DE是△ABC的中位线,∠B=60°,则∠ADE的度数为( )| A. | 80° | B. | 70° | C. | 60° | D. | 50° |
10.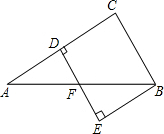 如图,△ABC中,AC的中垂线交AC、AB于点D、F,BE⊥DF交DF延长线于点E,若∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是( )
如图,△ABC中,AC的中垂线交AC、AB于点D、F,BE⊥DF交DF延长线于点E,若∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是( )
 如图,△ABC中,AC的中垂线交AC、AB于点D、F,BE⊥DF交DF延长线于点E,若∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是( )
如图,△ABC中,AC的中垂线交AC、AB于点D、F,BE⊥DF交DF延长线于点E,若∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是( )| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{2}$ | C. | 3$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
20.下列计算正确的个数是( )
①(x+y)2=x2+y2
②(-x+y)2=x2-2xy+y2
③(x+2y)(x-2y)=x2-2y2
④(-2a-3)(2a-3)=9-4a2
⑤(a-b)2=a2-b2.
①(x+y)2=x2+y2
②(-x+y)2=x2-2xy+y2
③(x+2y)(x-2y)=x2-2y2
④(-2a-3)(2a-3)=9-4a2
⑤(a-b)2=a2-b2.
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
4.下列等式成立的是( )
| A. | (a+b)2=a2+b2 | B. | (a-b)2=a2-b2 | C. | (x-4)(x+4)=x2-4 | D. | (a+b)2=a2+b2+2ab |