题目内容
10.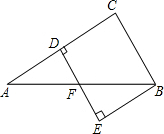 如图,△ABC中,AC的中垂线交AC、AB于点D、F,BE⊥DF交DF延长线于点E,若∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是( )
如图,△ABC中,AC的中垂线交AC、AB于点D、F,BE⊥DF交DF延长线于点E,若∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是( )| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{2}$ | C. | 3$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
分析 先证明△BCF是等边三角形,得出CF=BC=2,∠BCF=60°,求出CD,再证明四边形BCDE是矩形,即可求出面积.
解答 解:连接CF,如图所示:
∵DE是AC的中垂线,
∴AF=CF,∠CDE=90°,
∴∠ACF=∠A=30°,
∴∠CFB=∠A+∠ACF=60°,
∵AF=BF,
∴CF=BF,
∴△BCF是等边三角形,
∴CF=BC=2,∠BCF=60°,
∴CD=CF•cos30°=$\sqrt{3}$,∠BCD=60°+30°=90°,
∵BE⊥DF,
∴∠E=90°,
∴四边形BCDE是矩形,
∴四边形BCDE的面积=BC•CD=2×$\sqrt{3}$=2$\sqrt{3}$;
故选:A.
点评 本题考查了矩形的判定与性质、线段垂直平分线的性质、三角函数以及等边三角形的判定与性质;证明等边三角形和矩形是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.某天,一蔬菜经营户总共用180元钱从蔬菜批发市场批了西红柿和豆角共40kg到菜市场去买,西红柿和豆角这天的批发价与零售价如下表所示:
问:他当天卖完这些西红柿和豆角能赚多少钱?
| 品 名 | 西红柿 | 豆角 |
| 批发价(单位:元/kg) | 3.6 | 4.8 |
| 零售价(单位:元/kg) | 5 | 6 |
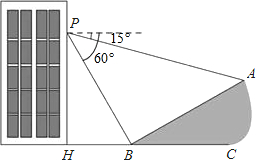 如图,小明在大楼30米高(即PH=30米)窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:$\sqrt{3}$,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC.求A、B两点间的距离.(结果精确到1米,参考数据:$\sqrt{3}$≈1.732).
如图,小明在大楼30米高(即PH=30米)窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:$\sqrt{3}$,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC.求A、B两点间的距离.(结果精确到1米,参考数据:$\sqrt{3}$≈1.732).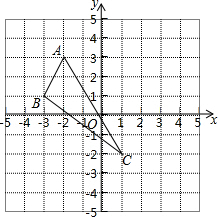 已知△ABC在平面直角坐标系中的位置如图所示
已知△ABC在平面直角坐标系中的位置如图所示