题目内容
14.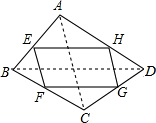 如图,在四边形ABCD中,点E.F.G.H分别为四边形ABCD各边的中点,顺次连接点E.F.G.H,
如图,在四边形ABCD中,点E.F.G.H分别为四边形ABCD各边的中点,顺次连接点E.F.G.H,(1)试判断四边形EFGH的形状,并证明你的结论.
(2)如果四边形ABCD是矩形,则四边形EFGH是什么形状?并说明理由.
分析 (1)根据三角形的中位线得到HG∥AC,HG=$\frac{1}{2}$AC,EF∥AC,EF=$\frac{1}{2}$AC,推出EF=GH,EF∥GH,根据平行四边形的判定求出即可.
(2)由三角形中位线定理得到FE=$\frac{1}{2}$AC,EF=$\frac{1}{2}$BD,则由矩形的对角线相等易推知平行四边形EFGH的邻边相等,故平行四边形EFGH是菱形.
解答  解:(1)四边形EFGH是平行四边形,理由如下:
解:(1)四边形EFGH是平行四边形,理由如下:
∵四边形ABCD各边中点是E、F、G、H,
∴HG∥AC,HG=$\frac{1}{2}$AC,EF∥AC,EF=$\frac{1}{2}$AC,
∴EF=GH,EF∥GH,
∴四边形EFGH是平行四边形.
(2)如果四边形ABCD是矩形,则四边形EFGH是菱形.理由如下:
由(1)知,四边形EFGH是平行四边形.
∵E、F分别是AB、BC边上的中点,
∴EF是△ABC的中位线,
∴FE=$\frac{1}{2}$AC,
同理,EH=$\frac{1}{2}$BD,
又∵四边形ABCD是矩形,
∴AC=BD,
∴EF=EH,
∴平行四边形EFGH是菱形.
点评 本题主要考查对平行四边形的判定,三角形的中位线,平行公理及推论等知识点的理解和掌握,能推出EF=GH和EF∥GH是解此题的关键.

练习册系列答案
相关题目
5.两个负数的差是正数,就必须符合( )
| A. | 被减数大 | B. | 被减数小 | C. | 两个数相等 | D. | 减数大 |
19.我市某天早上气温是-6℃中午上升了9℃,到了夜间又下降了12℃,这天我市夜间的温度是( )
| A. | 3℃ | B. | -3℃ | C. | 9℃ | D. | -9℃ |
3.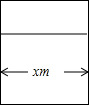 现有12m长的木料,要做成一个如图所示的窗框,若所做窗框横档的长度为xm,则窗框的高是( )
现有12m长的木料,要做成一个如图所示的窗框,若所做窗框横档的长度为xm,则窗框的高是( )
 现有12m长的木料,要做成一个如图所示的窗框,若所做窗框横档的长度为xm,则窗框的高是( )
现有12m长的木料,要做成一个如图所示的窗框,若所做窗框横档的长度为xm,则窗框的高是( )| A. | (6-x)m | B. | (12-x)m | C. | (6-3x)m | D. | (6-$\frac{3}{2}x$)m |
 观察图,并研究下列算式
观察图,并研究下列算式