题目内容
18.AD是△ABC的边BC上的中线,AB=6,AC=8,则中线AD的取值范围是1<AD<7.分析 延长AD到E,使AD=DE,连接BE,证△ADC≌△EDB,推出AC=BE=8,在△ABE中,根据三角形三边关系定理得出AB-BE<AE<AB+BE,代入求出即可.
解答 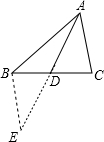 解:延长AD到E,使AD=DE,连接BE,
解:延长AD到E,使AD=DE,连接BE,
∵AD是BC边上的中线,
∴BD=CD,
在△ADC和△EDB中,
$\left\{\begin{array}{l}{AD=DE}\\{∠ADC=∠EDB}\\{DC=BD}\end{array}\right.$,
∴△ADC≌△EDB(SAS),
∴AC=BE=8,
在△ABE中,AB-BE<AE<AB+BE,
∴8-6<2AD<6+8,
∴1<AD<7,
故答案为:1<AD<7.
点评 本题考查了全等三角形的性质和判定,三角形的三边关系定理的应用,主要考查学生的推理能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.下列说法中,正确的个数有( ) 个.
①有理数包括整数和分数;
②一个代数式不是单项式就是多项式;
③几个有理数相乘,若负因数的个数是偶数个,则积为正数.
④倒数等于本身的数有1,-1.
①有理数包括整数和分数;
②一个代数式不是单项式就是多项式;
③几个有理数相乘,若负因数的个数是偶数个,则积为正数.
④倒数等于本身的数有1,-1.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
10.已知,线段a=1,b=4,且线段c是a、b的比例中项,则c为( )
| A. | ±2 | B. | 2 | C. | 3 | D. | 16 |
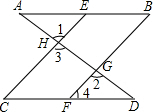 把下面的说理过程补充完整:
把下面的说理过程补充完整: