题目内容
19. 如图所示是某养殖专业户建立的一个矩形场地,一边靠墙,另三边除大门外用篱笆围成.已知篱笆总长为30m,门宽是2m,若设这块场地的宽为xm.
如图所示是某养殖专业户建立的一个矩形场地,一边靠墙,另三边除大门外用篱笆围成.已知篱笆总长为30m,门宽是2m,若设这块场地的宽为xm.(1)求场地的面积y(m2)与x(m)之间的函数关系式;
(2)写出自变量x的取值范围.
分析 (1)由篱笆总长为30m,门宽是2m,以及这块场地的宽为xm,得到这块场地的长为(32-2x)m,再利用矩形的面积公式即可列出矩形面积y与x的关系式;
(2)由场地的长32-2x>0,求出自变量x的取值范围即可.
解答 解:(1)由题意得y=x(32-2x)=-2x2+32x;
(2)∵32-2x>0,
∴x<16,
又∵x>0,
∴0<x<16.
点评 此题考查了根据实际问题列二次函数关系式,属于与实际生活密切相关的问题相联系的应用题,找出题中的等量关系是解决本题的关键;易错点是根据篱笆长得到这块场地的长.

练习册系列答案
相关题目
9.为了估计某城市空气质量情况,某同学在30天里做了如下记录:
其中w≤50时空气质量为优,50<w≤100时空气质量为良,100<w≤150时空气质量为轻度污染,若1年按365天计算,请你估计该城市在一年中空气质量达到良以上(含良)的天数为304天.
| 污染指数(w) | 40 | 60 | 80 | 100 | 120 | 140 |
| 天数(天) | 3 | 5 | 10 | 7 | 4 | 1 |
10.下列各式化简后,结果为无理数的是( )
| A. | $\sqrt{(-8)^{2}}$ | B. | $\root{3}{64}$ | C. | $\sqrt{9}$ | D. | $\sqrt{12}$ |
7.函数y=$\sqrt{x+2}$的自变量x的取值范围是( )
| A. | x≠-2 | B. | x≥-2 | C. | x>-2 | D. | x<-2 |
 如图,正方形ABCD的边长为3,以直线AB为轴,将正方形旋转一周,从正面看所得图形的周长是18.
如图,正方形ABCD的边长为3,以直线AB为轴,将正方形旋转一周,从正面看所得图形的周长是18.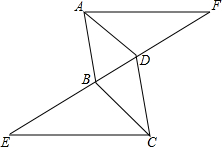 如图所示,△ADF≌△CBE,且点E,B,D,F在一条直线上,判断AD与BC的位置关系,并说明理由.
如图所示,△ADF≌△CBE,且点E,B,D,F在一条直线上,判断AD与BC的位置关系,并说明理由.