题目内容
12.已知A(-2,2),B(0,3),若要在x轴上找一点P,使AP+BP最短,由此得点P的坐标为(-$\frac{6}{5}$,0).分析 根据题意画出坐标系,在坐标系内找出A、B两点,作点B关于x轴的对称点C,连接AC交x轴于点P,求出P点坐标即可.
解答 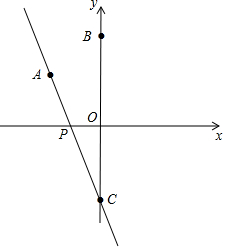 解:点B关于x轴的对称点C,连接AC交x轴于点P,
解:点B关于x轴的对称点C,连接AC交x轴于点P,
则AP+BP最短,
∵B(0,3),
∴C(0.-3),
设直线AC的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{2=-2k+b}\\{-3=b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{5}{2}}\\{b=-3}\end{array}\right.$,
∴直线AC的解析式为y=-$\frac{5}{2}$x-3,
当y=0时,x=-$\frac{6}{5}$,
∴P(-$\frac{6}{5}$,0).
故答案为:(-$\frac{6}{5}$,0).
点评 本题考查的是轴对称-最短路线问题,熟知“两点之间,线段最短”是解答此题的关键.

练习册系列答案
相关题目
20.抛物线y=(1-3x)2+2的对称轴是( )
| A. | x=3 | B. | x=-3 | C. | $x=\frac{1}{3}$ | D. | $x=-\frac{1}{3}$ |
7.如果把分式$\frac{2a+b}{2ab}$中的a和b都扩大了2倍,那么分式的值( )
| A. | 扩大2倍 | B. | 不变 | C. | 缩小2倍 | D. | 缩小4倍 |
2.a的2倍与b的$\frac{1}{3}$的差的平方,用代数式表示应为( )
| A. | 2a2-$\frac{1}{3}$b2 | B. | 2a2-$\frac{1}{3}$b | C. | (2a-$\frac{1}{3}$b)2 | D. | 2a-($\frac{1}{3}$b)2 |