题目内容
在直角Rt△ABC中，∠C=90°，∠B=15°，BC=2+| 3 |
考点：勾股定理
专题：
分析：过点A作AD交BC于点D，∠CAD=60°，则∠ADC=30°，根据∠B=15°可知∠B=∠BAD=15°，故可得出AD=BD，再由直角三角形的性质可得出AC的长．
解答：
解：过点A作AD交BC于点D，∠CAD=60°，则∠ADC=30°，
∵∠B=15°，
∴∠B=∠BAD=15°，
∴AD=BD．
∴∠ADC=30°．
∵BD+CD=2+
，
∴BD=AD=2AC，CD=
AC，
∴2AC+
AC=2+
，即AC=1．
解：过点A作AD交BC于点D，∠CAD=60°，则∠ADC=30°，∵∠B=15°，
∴∠B=∠BAD=15°，
∴AD=BD．
∴∠ADC=30°．
∵BD+CD=2+
| 3 |
∴BD=AD=2AC，CD=
| 3 |
∴2AC+
| 3 |
| 3 |
点评：本题考查的是勾股定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
七星图书口算速算天天练系列答案
相关题目
如图，点D是△ABC的边AC的上一点，且∠ABD=∠C；如果
如图，E是平行四边形ABCD边BC上的一点，且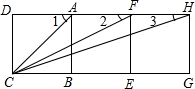
如图所示，三个边长为1个单位长度的正方形ABCD、ABEF、EFHG拼在一起．