题目内容
Rt△ABC中，∠C=90°，∠A、∠B、∠C的对边分别为a、b、c，且a：b=3：4，斜边c=15，则b的值是（ ）
| A、12 | B、9 | C、4 | D、3 |
考点：勾股定理
专题：
分析：设a=3x，则b=4x，再根据勾股定理求出x的值，进而可得出结论．
解答：解：∵Rt△ABC中，∠C=90°，∠A、∠B、∠C的对边分别为a、b、c，且a：b=3：4，
∴设a=3x，则b=4x．
∵a2+b2=c2，即（3x）2+（4x）2=152，解得x=3，
∴b=4x=12．
故选A．
∴设a=3x，则b=4x．
∵a2+b2=c2，即（3x）2+（4x）2=152，解得x=3，
∴b=4x=12．
故选A．
点评：本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
相关题目
如图所示，有两根木杆，甲杆长80cm，乙杆长60cm，某一时刻，甲、乙两杆均垂直于地面，甲杆的影长40cm，乙杆在墙面上的影长是10cm，问乙杆的底端D离墙脚的距离是多少？下列各组中，是同类项的是（ ）
| A、-x2y与3yx2 |
| B、m3与3m |
| C、a2与b2 |
| D、x与2 |
在直角Rt△ABC中，∠C=90°，∠B=15°，BC=2+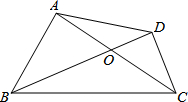
如图，已知在四边形ABCD中，AC与BD相交于点O，AB⊥AC，CD⊥BD．