题目内容
如图:已知AB=AE,BC=ED,∠B=∠E,AF⊥CD,F为垂足,求证:①AC=AD; ②CF=DF.

【考点】等腰三角形的判定;全等三角形的判定与性质.
【专题】证明题.
【分析】由已知可利用SAS判定△ABC≌△AED,根据全等三角形的对应边相等可得到AC=AD,即△ACD是等腰三角形,已知AF⊥CD,则根据等腰三角形三线合一的性质即可推出CF=DF.
【解答】证明:①∵AB=AE,BC=ED,∠B=∠E,
∴△ABC≌△AED(SAS),
∴AC=AD,
②∵AF⊥CD,AC=AD,
∴CF=FD(三线合一性质).
【点评】此题主要考查等腰三角形的判定及全等三角形的判定与性质的综合运用.

练习册系列答案
相关题目



 5°,则∠BCD的度数为 度.
5°,则∠BCD的度数为 度.
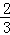 ;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.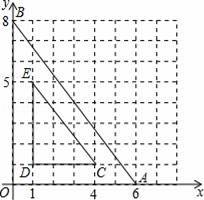

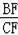
 的值.
的值.
