题目内容
如图,已知△ABC中,AB=AC,AD=AE,∠BAE=30°,则∠DEC等于( )

A.7.5° B.10° C.15° D.18°
C【考点】等腰三角形的性质;三角形内角和定理;三角形的外角性质.
【专题】计算题.
【分析】根据等腰三角形性质求出∠C=∠B,根据三角形的外角性质求出∠B=∠C=∠AED+α﹣30°,根据∠AED=∠ADE=∠C+α,得出等式∠AED=∠AED+α﹣30°+α,求出即可.
【解答】解:∵AC=AB,
∴∠B=∠C,
∵∠AEC=∠B+∠BAE=∠B+30°=∠AED+α,
∴∠B=∠C=∠AED+α﹣30°,
∵AE=AD,
∴∠AED=∠ADE=∠C+α,
即∠AED=∠AED+α﹣30°+α,
∴2α=30°,
∴α=15°,
∠DEC=α=15°,
故选C.
【点评】本题考查了等腰三角形的性质,三角形的内角和定理,三角形的外角性质等知识点的应用,主要考查学生运用定理进行推理的能力,本题有一点难度,但题型不错.

练习册系列答案
相关题目



 B.
B.
 C.
C.
 D.
D.


 ,化简
,化简 +|a﹣2|的结果是( )
+|a﹣2|的结果是( )
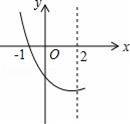

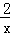 ,下列说法正确的是( )
,下列说法正确的是( )