题目内容
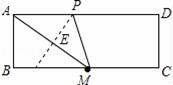
如图,在矩形ABCD中,AB=5,BC=24,M是BC的中点,若点P为线段AD上的一点,连接AM、PM,△PAM是以AP为腰的等腰三角形,则AP的长为 .


13或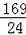
 .
.
【考点】矩形的性质;等腰三角形的判定;勾股定理.
【专题】分类讨论.
【分析】分两种情况:①当AP=AM时,根据勾股定理求出AM即可得出AP;
(2)当AP=MP时,P在AM的垂直平分线上,证明△PEA∽△ABM,得出对应边成比例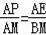
 ,即可求出AP.
,即可求出AP.
【解答】解:分两种情况:①当AP=AM时,
∵四边形ABCD是矩形,
∴∠B=∠BAD=90°,AD∥BC,
∵M是BC的中点,
∴BM=
 BC=12,
BC=12,
∴AM=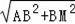
 =
=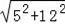
 =13,
=13,
∴AP=13;
(2)当AP=MP时,P在AM的垂直平分线上,如图所示:
则∠AEP=90°=∠B,AE=
 AM=
AM=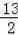
 ,
,
∵AD∥BC,
∴∠PAE=∠AMB,
∴△PEA∽△ABM,
∴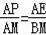
 ,即
,即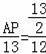
 ,
,
解得:AP=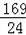
 ;
;
故答案为:13或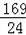
 .
.

【点评】本题考查了矩形的性质、等腰三角形的性质、勾股定理以及相似三角形的判定与性质;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
 ,求GC的长.
,求GC的长.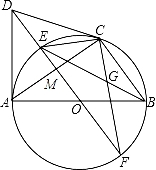



 B.
B.
 C.
C.
 D.
D.


 中自变量x的取值范围是 .
中自变量x的取值范围是 .

 ,化简
,化简 +|a﹣2|的结果是( )
+|a﹣2|的结果是( )