题目内容
14.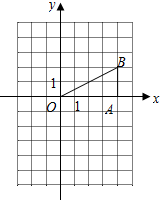 如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴于A.
如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴于A.(1)求tan∠BOA的值;
(2)将△OAB平移得到△O′A′B′,点A的对应点是A′,点B的对应点B′的坐标为(2,-2),在坐标系中作出△O′A′B′,并写出点O′、A′的坐标.
分析 (1)根据锐角三角函数的定义可得出tan∠BOA的值;
(2)直接根据图形平移的性质画出平移后的△O′A′B′,根据点O′、A′在坐标系中的位置写出其坐标即可.
解答 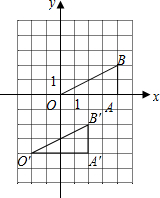 解:(1)∵AB=2,OA=4,
解:(1)∵AB=2,OA=4,
∴tan∠BOA=$\frac{AB}{OA}$=$\frac{2}{4}$=$\frac{1}{2}$;
(2)如图所示,O′(-2,-4),A′(2,4).
点评 本题考查的是作图-平移变换,熟知图形平移不变性的性质是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.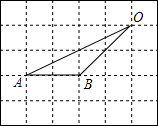 如图,在网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是( )
如图,在网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是( )
 如图,在网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是( )
如图,在网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是( )| A. | $\frac{10\sqrt{10}}{3}$ | B. | $\frac{\sqrt{10}}{10}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
3. 如图,△ODC是由△OAB绕点O顺时针旋转31°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠DOB的度数是( )
如图,△ODC是由△OAB绕点O顺时针旋转31°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠DOB的度数是( )
 如图,△ODC是由△OAB绕点O顺时针旋转31°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠DOB的度数是( )
如图,△ODC是由△OAB绕点O顺时针旋转31°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠DOB的度数是( )| A. | 34° | B. | 36° | C. | 38° | D. | 40° |
4.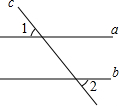 已知:如图,直线a∥b,若∠1=66°,则∠2的度数为( )
已知:如图,直线a∥b,若∠1=66°,则∠2的度数为( )
 已知:如图,直线a∥b,若∠1=66°,则∠2的度数为( )
已知:如图,直线a∥b,若∠1=66°,则∠2的度数为( )| A. | 66° | B. | 68° | C. | 76° | D. | 89° |
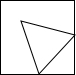
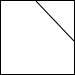
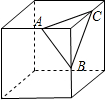 如图,是一个切去了一个角的正方体,切面与棱的交点A,B,C均是棱的中点,得到的几何体的主视图是( )
如图,是一个切去了一个角的正方体,切面与棱的交点A,B,C均是棱的中点,得到的几何体的主视图是( )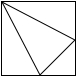

 如图是长方形鸡场平面示意图,一边靠墙(墙足够长),另外三边用竹篱笆围成,在其中一边上有一个1米长的小门(用其它材料制成),若竹篱笆总长为34米,所围的面积为150平方米,求此长方形鸡场的长、宽分别为多少米?
如图是长方形鸡场平面示意图,一边靠墙(墙足够长),另外三边用竹篱笆围成,在其中一边上有一个1米长的小门(用其它材料制成),若竹篱笆总长为34米,所围的面积为150平方米,求此长方形鸡场的长、宽分别为多少米?