题目内容
6.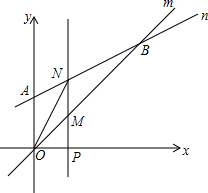 如图,在平面直角坐标系中,直线m:y=kx过原点,直线n:y=$\frac{1}{2}$x+4与y轴交于点A,与直线m交于点B(8,8),x轴上一点P(t,0)从原点出发沿x轴向右运动,过点P作直线PM⊥x轴,分别交直线m,n与点M,N,连接ON.
如图,在平面直角坐标系中,直线m:y=kx过原点,直线n:y=$\frac{1}{2}$x+4与y轴交于点A,与直线m交于点B(8,8),x轴上一点P(t,0)从原点出发沿x轴向右运动,过点P作直线PM⊥x轴,分别交直线m,n与点M,N,连接ON.(1)求k的值;
(2)当0≤t≤8时,用含t的代数式表示△OMN的面积S;
(3)在整个运动过程中,△OMN的面积S等于12吗?如果能,请求出t的值;如果不能,请说明理由;
(4)当t为何值时,以MN为直径的圆与y轴相切?
分析 (1)根据待定系数法,可得答案;
(2)根据自变量的值,可得相应的函数值,根据三角形的面积公式,可得答案;
(3)分类讨论:当0≤t≤8时,当t>8时,根据三角形的面积,可得关于t的方程,根据解方程,可得答案;
(4)分类讨论:当0≤t≤8时,当t>8时,根据相切,可得OP与MN的关系,根据解方程,可得答案.
解答 解:(1)将B点(8,8)代入y=kx,得
k=$\frac{y}{x}$=1;
(2)当x=t时,y=$\frac{1}{2}$t+4,即N(t,$\frac{1}{2}$t+4);y=t,即M(t,t).
NM=$\frac{1}{2}$t+4-t=4-$\frac{1}{2}$t,
S△OMN=$\frac{1}{2}$MN•OP=$\frac{1}{2}$(4-$\frac{t}{2}$)•t=2t-$\frac{1}{4}$t2;
(3)当0≤t≤8时,S△OMN=2t-$\frac{1}{4}$t2=12,
化简,得
t2-8t+48=0,
△=b2-4ac=64-4×48=-128,
方程无解;
当t>8时,S△OMN=$\frac{1}{4}$t2-2t=12,
解得t=12,t=-4(不符合题意舍),
综上所述:t=12时,△OMN的面积S等于12;
(4)以MN为直径的圆与y轴相切,得
2OP=MN.
当0≤t≤8时,2t=4-$\frac{1}{2}$t,
解得t=$\frac{8}{5}$,
即t=$\frac{8}{5}$时,以MN为直径的圆与y轴相切;
当t>8时,2t=$\frac{1}{2}$t-4,
解得t=-$\frac{8}{3}$(不符合题意舍),
综上所述:当t=$\frac{8}{5}$时,以MN为直径的圆与y轴相切.
点评 本题考查了一次函数综合题,利用待定系数法求函数解析式,三角形的面积公式,直线与圆相切的关系,分类讨论是阶梯关键,以防遗漏.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案| A. | 2011 | B. | 2012 | C. | 2013 | D. | 2014 |
| A. | x2 | B. | $\frac{1}{2}{x}^{2}$ | C. | $\frac{1}{3}{x}^{2}$ | D. | $\frac{1}{4}$x2 |
| A. | 2x+y=6z | B. | $\frac{1}{x}$+2=3y | C. | 3x-2y=9 | D. | x-3=4y2 |
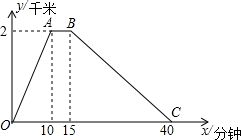 李老师每天坚持晨跑.如图反映的是李老师某天6:20从家出发小跑到赵化北门,在北门休息几分钟后又慢跑回家的函数图象.其中x(分钟)表示所用时间,y(千米)表示李欢离家的距离.
李老师每天坚持晨跑.如图反映的是李老师某天6:20从家出发小跑到赵化北门,在北门休息几分钟后又慢跑回家的函数图象.其中x(分钟)表示所用时间,y(千米)表示李欢离家的距离.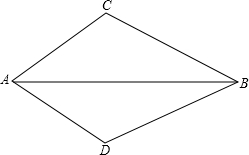 利用构造全等直角三角形证线段相等:如图,∠C=∠D,AC=AD,求证:BC=BD.
利用构造全等直角三角形证线段相等:如图,∠C=∠D,AC=AD,求证:BC=BD.