题目内容
9．
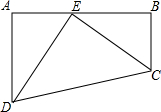如图，四边形ABCD中，∠A=∠B=90°，AB=25，AD=15，BC=10，点E是AB上一点，且DE=CE，求AE的长．
分析 设AE=x，表示出BE=25-x，再分别利用勾股定理列式表示出DE2、CE2，然后根据DE=CE列方程求解即可．
解答 解：设AE=x，
∵AB=25，
∴BE=25-x，
∵∠A=∠B=90°，
∴DE2=AD2+AE2=152+x2，
CE2=BC2+BE2=102+（25-x）2，
∵DE=CE，
∴152+x2=102+（25-x）2，
解得x=10，
所以，AE=10．
点评 本题考查了勾股定理，熟记定理并准确识图，根据DE=CE列出方程是解题的关键．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
如图，在?ABCD中，点G在边BC的延长线上，AG与边CD交于点E，与对角线BD交于点F，求证：AF2=EF•FG．
已知，如图AB=AE，∠B=∠E，BC=ED，AF平分∠BAE，求证：AF⊥CD．
如图，将一块长方形纸条折成如图的形状，若已知∠1=110°，则∠2=55°．