题目内容
1.电子跳蚤落在数轴上的某点k0处,第一步从k0向左跳1个单位到k1,第二步由k1向右跳2个单位到k2,第三步由k2向左跳3个单位到k3,第四步由k3向右跳4个单位到k4,…,按以上规律跳了100步时,电子跳蚤落在数轴上的点k100所表示的数恰是51,试问电子跳蚤的初始位置点k0表示的数是多少?分析 设电子跳蚤落在数轴上的某点K0=a,规定向左为负,向右为正,根据题意列出方程,再进一步根据有理数的加法法则进行计算.
解答 解:设电子跳蚤落在数轴上的某点K0=a,规定向左为负,向右为正.
根据题意,得:a-1+2-3+4-…+100=51,
a+(2-1)+…+(100-99)=51,
a+50=51,
解得:a=1.
即电子跳蚤的初始位置点k0表示的数是1.
点评 此题考查了数轴、正负数的意义,能够借助正负数来表示题目中的运动,同时注意运用简便方法进行计算.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
11.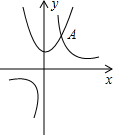 如图,抛物线y=x2+2与双曲线y=$\frac{k}{x}$的交点A的横坐标是2,则关于x的不等式$\frac{k}{x}$+x2+2<0的解是( )
如图,抛物线y=x2+2与双曲线y=$\frac{k}{x}$的交点A的横坐标是2,则关于x的不等式$\frac{k}{x}$+x2+2<0的解是( )
 如图,抛物线y=x2+2与双曲线y=$\frac{k}{x}$的交点A的横坐标是2,则关于x的不等式$\frac{k}{x}$+x2+2<0的解是( )
如图,抛物线y=x2+2与双曲线y=$\frac{k}{x}$的交点A的横坐标是2,则关于x的不等式$\frac{k}{x}$+x2+2<0的解是( )| A. | 0<x<2 | B. | -2<x<0 | C. | x>2 | D. | x<-2 |
10.下列说法正确的是( )
| A. | 只有符号不同的两个数互为相反数 | B. | 有理数分为正有理数和负有理数 | ||
| C. | 两数相加,和一定大于任何一数 | D. | 零是自然数,但不是有理数 |
13.10.8减去(-7.4)的差是( )
| A. | 3.4 | B. | -3.4 | C. | 18.2 | D. | -18.2 |
