题目内容
13.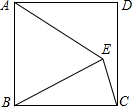 如图,以正方形ABCD的边AB为一边向内作等边△ABE,连结EC,则∠AEC的度数为( )
如图,以正方形ABCD的边AB为一边向内作等边△ABE,连结EC,则∠AEC的度数为( )| A. | 120° | B. | 135° | C. | 145° | D. | 150° |
分析 在正方形ABCD中,△ABE是等边三角形,可求出∠AEB、∠ABE的大小以及推断出BC=BE,从而可求出∠BEC,再根据角的和差关系求出∠AEC的度数.
解答 解:如图,在正方形ABCD中,∠ABC=90°,AB=BC.
∵△ABE是等边三角形,
∴∠AEB=∠ABE=60°,AB=BE,
∴∠EBC=90°-60°=30°,BE=BC,
∴∠BCE=∠BEC=$\frac{1}{2}$(180°-30°)=75°,
∴∠AEC=∠AEB+∠BEC=60°+75°=135°.
故选:B.
点评 本题考查了正方形的性质、等边三角形的性质.根据正方形和等边三角形的性质推知BE=BC是解题的关键.

练习册系列答案
相关题目
3. 如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于$\frac{1}{2}$BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD,若CD=AC,∠B=25°,则∠ACB的度数为( )
如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于$\frac{1}{2}$BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD,若CD=AC,∠B=25°,则∠ACB的度数为( )
 如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于$\frac{1}{2}$BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD,若CD=AC,∠B=25°,则∠ACB的度数为( )
如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于$\frac{1}{2}$BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD,若CD=AC,∠B=25°,则∠ACB的度数为( )| A. | 105° | B. | 100° | C. | 95° | D. | 90° |
4.已知圆锥的底面半径为4,母线长为12,则圆锥的侧面展开图的圆心角为( )
| A. | 60° | B. | 90° | C. | 120° | D. | 216° |
1.若分式$\frac{x+2}{x-1}$有意义,则x的取值范围是( )
| A. | x≥1 | B. | x≠1 | C. | x≥-2 | D. | x≠-2 |
8.估计$\sqrt{14}$的值在哪两个数之间( )
| A. | 1与2 | B. | 2 与3 | C. | 3与4 | D. | 4与5 |
18.下列根式中不是最简二次根式的是( )
| A. | $\sqrt{10}$ | B. | $\sqrt{12}$ | C. | $\sqrt{14}$ | D. | $\frac{\sqrt{17}}{2}$ |
4.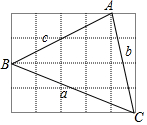 如图所示,在正方形网格中,每个小正方形的边长为1,则网格上的△ABC(△ABC的各项点均在格点上)的三边a、b、c之间的大小关系是( )
如图所示,在正方形网格中,每个小正方形的边长为1,则网格上的△ABC(△ABC的各项点均在格点上)的三边a、b、c之间的大小关系是( )
 如图所示,在正方形网格中,每个小正方形的边长为1,则网格上的△ABC(△ABC的各项点均在格点上)的三边a、b、c之间的大小关系是( )
如图所示,在正方形网格中,每个小正方形的边长为1,则网格上的△ABC(△ABC的各项点均在格点上)的三边a、b、c之间的大小关系是( )| A. | c<a<b | B. | b<c<a | C. | c<b<a | D. | a<c<b |
 如图,以等腰三角形ABC的底边BC为直径的圆O分别交两腰于D、E,连结DE,求证:
如图,以等腰三角形ABC的底边BC为直径的圆O分别交两腰于D、E,连结DE,求证: