题目内容
19．
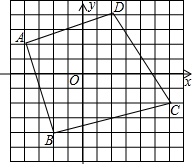已知，如图，四边形ABCD的顶点坐标分别为A（-4，2），B（-2，-4），C（6，-2），D（2，4），试以O点为位似中心作四边形A′B′C′D′，使四边形ABCD与四边形A′B′C′D′的位似比为2：1（只画一种情况）．（1）写出所画四边形A′B′C′D′各顶点的坐标；
（2）四边形A′B′C′D′的面积是12．
分析 （1）直接利用位似图形的性质结合位似比得出对应点坐标即可；
（2）利用四边形A′B′C′D′所在矩形减去周围三角形面积进而得出即可．
解答 
解：（1）如图所示：
A′（-2，1），B′（-1，-2），C′（3，-1），D′（1，2）；
（2）四边形A′B′C′D′的面积是：
4×5-$\frac{1}{2}$×1×3-$\frac{1}{2}$×1×3-$\frac{1}{2}$×1×4-$\frac{1}{2}$×2×3
=12．
故答案为：12．
点评 此题主要考查了位似变换以及四边形面积求法，利用位似图形的性质得出对应点位置是解题关键．
练习册系列答案
相关题目
