题目内容
11．
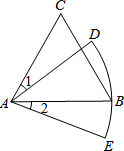如图，△ABC是等边三角形，AC=6，以点A为圆心，AB长为半径画弧DE，若∠1=∠2，则弧DE的长为（ ）| A． | 1π | B． | 1.5π | C． | 2π | D． | 3π |
分析 先由等边三角形的性质得出AB=AC=6，∠CAB=60°．再由∠1=∠2得到∠CAB=∠DAE=60°，然后根据弧长公式解答即可．
解答 解：∵△ABC是等边三角形，AC=6，
∴AB=AC=6，∠CAB=60°．
∵∠1=∠2，
∴∠1+∠BAD=∠2+∠BAD，
∴∠CAB=∠DAE=60°，
∴弧DE的长为$\frac{60×π×6}{180}$=2π，
故选C．
点评 本题考查了扇形的弧长，等边三角形的性质，找到圆心角∠DAE的度数是解题的关键．
练习册系列答案
相关题目
1．
如图，如果数轴上A，B两点之间的距离是8，那么点B表示的数是（ ）
如图，如果数轴上A，B两点之间的距离是8，那么点B表示的数是（ ）| A． | -5 | B． | -3 | C． | 3 | D． | 5 |
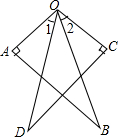如图，OA⊥AB，OC⊥CD，OA=OC，OB=OD，求证：∠1=∠2．
尼泊尔地震牵动着全中国人民的心，中国红十字基金会开展了“一方有难，八方支援”的赈灾活动．5月15日，中国红十字基金会联手北京成龙慈善基金会等共同出资400万元人民币，采购5000只“赈济家庭箱”（“赈济家庭箱”包括当地受灾群众急需的毛毯、防潮垫、睡袋、雨衣、服装、餐具、个人护理用品等），作为首批物资援助尼泊尔地震灾区．该基金会计划到第三批援助物资为止共采购18200只“赈济家庭箱”．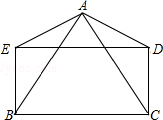
如图，AB=AC，AD=AE，DE=BC，且∠BAD=∠CAE．
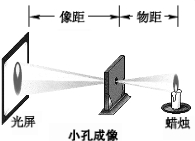两千多年前，我国的学者墨子和他的学生做了小孔成像的实验．他的做法是，在一间黑暗的屋子里，一面墙上开一个小孔，小孔对面的墙上就会出现外面景物的倒像．小华在学习了小孔成像的原理后，利用如图装置来验证小孔成像的现象．已知一根点燃的蜡烛距小孔20cm，光屏在距小孔30cm处，小华测量了蜡烛的火焰高度为2cm，则光屏上火焰所成像的高度为3cm．
1．$\sqrt{2}$-1的倒数为（ ）
| A． | $\sqrt{2}$-1 | B． | 1-$\sqrt{2}$ | C． | $\sqrt{2}$+1 | D． | -$\sqrt{2}$-1 |