题目内容
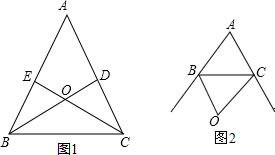 (1)已知;△ABC中,BD、CE是∠B、∠C的角平分线,并交于点O.求证:∠BOC=90°+
(1)已知;△ABC中,BD、CE是∠B、∠C的角平分线,并交于点O.求证:∠BOC=90°+| 1 |
| 2 |
(2)将上题中内角改成外角平分线,如图2,∠BOC与∠A有何关系,请你探究及证明.
考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)利用角平分线的性质求出∠2+∠4的度数,再由三角形的内角和定理便可求出∠BOC;
(2)根据三角形外角平分线的性质可得∠BCO=
(∠A+∠ABC)、∠OBC=
(∠A+∠ACB);根据三角形内角和定理可得∠BOC=90°-
∠A.
(2)根据三角形外角平分线的性质可得∠BCO=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: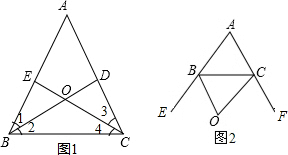 (1)证明:∵∠ABC和∠ACB的平分线BD、CE相交于点O,
(1)证明:∵∠ABC和∠ACB的平分线BD、CE相交于点O,
∴∠1=∠2,∠3=∠4,
∴∠2+∠4=
(180°-∠A)=90°-
∠A,
∴∠BOC=180°-(∠2+∠4)=180°-(90°-
∠A)=90°+
∠A;
(2))∠BOC=90°-
∠A.
证明:∵BO、CO为△ABC两外角∠CBE、∠BCF的平分线,∠A为x°
∴∠BCO=
(∠A+∠ABC)、∠OBC=
(∠A+∠ACB),
由三角形内角和定理得,∠BOC=180°-∠BCO-∠OBC,
=180°-
[∠A+(∠A+∠ABC+∠ACB)],
=180°-
(∠A+180°),
=90°-
∠A.
 (1)证明:∵∠ABC和∠ACB的平分线BD、CE相交于点O,
(1)证明:∵∠ABC和∠ACB的平分线BD、CE相交于点O,∴∠1=∠2,∠3=∠4,
∴∠2+∠4=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-(∠2+∠4)=180°-(90°-
| 1 |
| 2 |
| 1 |
| 2 |
(2))∠BOC=90°-
| 1 |
| 2 |
证明:∵BO、CO为△ABC两外角∠CBE、∠BCF的平分线,∠A为x°
∴∠BCO=
| 1 |
| 2 |
| 1 |
| 2 |
由三角形内角和定理得,∠BOC=180°-∠BCO-∠OBC,
=180°-
| 1 |
| 2 |
=180°-
| 1 |
| 2 |
=90°-
| 1 |
| 2 |
点评:本题考查的是三角形内角和定理,涉及到三角形内角与外角的关系,角平分线的性质,三角形内角和定理,属中学阶段的常规题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
下列各式中运算正确的是( )
| A、6a-5a=1 |
| B、a2+a2=a4 |
| C、3ab-4ba=-ab |
| D、3a+2b=5ab |
 如图,∠CAD和∠CBD的角平分线相交于点P,PA交BD于E,BP交AC于F,∠D=45°,∠P=60°,则∠C的度数是多少?
如图,∠CAD和∠CBD的角平分线相交于点P,PA交BD于E,BP交AC于F,∠D=45°,∠P=60°,则∠C的度数是多少? 如图,抛物线y=ax2-5x+4a与x轴相交于点A,B,且过点C(5,4),求a的值和该抛物线顶点P的坐标.
如图,抛物线y=ax2-5x+4a与x轴相交于点A,B,且过点C(5,4),求a的值和该抛物线顶点P的坐标.