题目内容
定义[p,q]为一次函数y=px+q的特征数.设点A,B分别为抛物线y=(x+m)(x-2)与x,y轴的交点,其中m>0,且△OAB的面积为4,O为原点,图象过A,B两点的一次函数的特征数为 .
考点:二次函数的性质,一次函数的性质
专题:新定义
分析:根据解析式易得抛物线与x轴、y轴的交点的坐标,又有△OAB的面积为4,可得m的方程,解即可得m的值,进而可得答案.
解答:解:抛物线与x轴的交点为A1(-m,0),A2(2,0),
与y轴的交点为B(0,-2m).
若S△OBA1=4,则
•m•2m=4,m=2.
若S△OBA2=4,则
•2•2m=4,m=2.
∴当m=2时,满足题设条件.
∴此时抛物线为y=(x+2)(x-2).
它与x轴的交点为(-2,0),(2,0),与y轴的交点为(0,-4),
∴一次函数为y=-2x-4或y=2x-4,
∴特征数为[-2,-4]或[2,-4].
故答案为:[-2,-4]或[2,-4].
与y轴的交点为B(0,-2m).
若S△OBA1=4,则
| 1 |
| 2 |
若S△OBA2=4,则
| 1 |
| 2 |
∴当m=2时,满足题设条件.
∴此时抛物线为y=(x+2)(x-2).
它与x轴的交点为(-2,0),(2,0),与y轴的交点为(0,-4),
∴一次函数为y=-2x-4或y=2x-4,
∴特征数为[-2,-4]或[2,-4].
故答案为:[-2,-4]或[2,-4].
点评:本题考查一次函数、二次函数的性质,解题的重点是能够根据新定义整理出一次函数、二次函数的模型,难度不大.

练习册系列答案
 能力评价系列答案
能力评价系列答案
相关题目
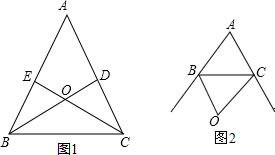 (1)已知;△ABC中,BD、CE是∠B、∠C的角平分线,并交于点O.求证:∠BOC=90°+
(1)已知;△ABC中,BD、CE是∠B、∠C的角平分线,并交于点O.求证:∠BOC=90°+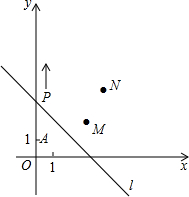 如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒.
如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒. 如图,已知△ABC中∠ABC和∠ACB的角平分线交于点I,若∠A=50°,则∠BIC=
如图,已知△ABC中∠ABC和∠ACB的角平分线交于点I,若∠A=50°,则∠BIC=